A műholdak pályája
A műholdpálya alakja
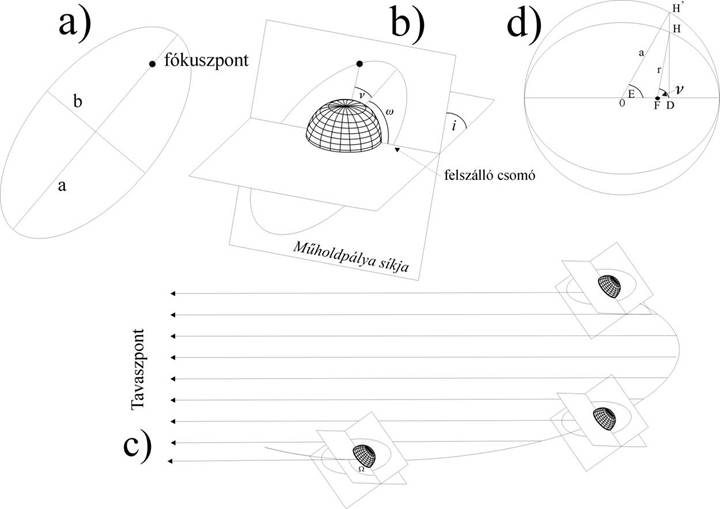
A pálya alakja a Kepler törvények értelmében kúpszelet (parabola, hiperbola vagy ellipszis) alakú, amelynek fókuszpontjában van a Föld tömegközéppontja. (A pályasíknak mindenképpen tartalmaznia kell a vonzó centrumot.) Amennyiben az égésvégi sebesség eléri a 11,2 km/s-ot (vagyis a 2. kozmikus sebességet) akkor a pálya parabola alakú nyílt pályává válik. Az 1. és 2. kozmikus sebességek közötti sebességértékek esetén a pálya ellipszis alakú (a körpálya ennek speciális esete).
A geometriából ismert, hogy egy ellipszis alakját többféle paraméterrel megadhatjuk. A csillagászatban és az űrkutatásban elterjedt módon az ellipszis alakú pályákat fél nagytengelyük (a) és excentricitásuk segítségével adjuk meg. Az excentricitás (e) a fókuszpontok távolsága felének és a fél nagytengelynek a hányadosa (lásd az ábra a.) pontját).

A műholdpálya helyzete a Földhöz képest
A műholdpályának a Földhöz viszonyított térbeli helyzetét leíró következő paraméter a pálya síkjának az egyenlítő síkjával bezárt szöge az inklináció (i). Az inklinációt a felszálló csomóban mérik (lásd az ábra b.) pontját), vagyis ahol a műhold a déli irányból észak felé haladva átlépi az egyenlítőt. Az inklináció értéke szerint megkülönböztetünk egyenlítői pályát (i=0), normál pályát (0<i<90), poláris pályát (i=90), illetve retrográd pályát (90<i<180). A poláris pályán a műhold a sarkok felett halad el, a retrográd pályán pedig a műhold Föld körüli keringése a Föld forgásásával ellentétes irányú.
Az inklinációval megadott pályasíkban az ellipszis alakú pálya földközeli pontjának a helyét a perigeum (földközeli pont) argumentuma (ω) adja meg. (Például ha egy poláris pályán az ω=90º, akkor az egy olyan műholdpályát ír le, ahol az Északi sarok felett elhaladva van a műhold a Földközeli, a Déli pólus felett elhaladva a földtávoli pontban.)
Ezek a pályaparaméterek együttesen leírják a műholdpályának a Földhöz viszonyított helyzetét.
A műholdpálya helyzete az állócsillagokhoz képest
A műholdpályának az állócsillagokhoz viszonyított helyzetét a felszálló csomó hossza (Ω) határozza meg (lásd az ábra c.) pontját). A felszálló csomó hossza, a Tavaszpont és a felszálló csomó szöge a Föld közeppontjából nézve, az egyenlítő síkjában mérve. A Tavaszpont a Földi egyenlítő síkjának a Föld keringési síkjával (az ekliptikával) alkotott metszetének egyik végpontjának iránya, amelyikben a Nap a tavaszi napéjegyenlőség idején tartózkodik.
A műhold pillanatnyi helyzete a pályán
A műholdnak az ellipszispályán elfoglalt pillantnyi helyzetét Kepler második törvényének segítségével határozhatjuk meg. Ennek értelmében, a vetítősugár (a Föld középpontjától a műholdig húzott szakasz) egyenlő idő alatt egyenlő területet súrol.
Ezt a területnövekedést írja le a középanomália (E). A középanomáliából geometriai megfontolások segítségével határozható meg a valódi anomália (ν), ami a vetítősugárnak a perigeumtól mért szöge (lásd az ábra d.) pontját).
Műholdak perturbált mozgása
A műholdra a mozgása során a centrálisnak tekintett gravitációs erőn kívül más – ún. perturbáló – erők is hatnak. Ezek hatására a különböző pályaparamétek időben változnak. Tetszőleges pillanatra felírhatók a perturbáló erők hatását is figyelembe vevő aktualizált pályaparaméterek.
A gyakorlatban ezeket napi rendszerességgel számítja, és teszi közzé a műhold üzemeltetője. A számított pályaparaméterek és a pályán elfoglalt pillanatnyi helyzet egy időpillanatra (az ún epochára) vonatkozik, amit ugyancsak megadnak.
A műhold mozgása eszerint úgy tekinthető, mintha a mozgáshoz rendelhető pályaparaméterek folyamatosan változnának: ezek a változó pályaparaméterek írják le a perturbált pályát. Ezen perturbáló erők rövid és hosszú periódusú perturbációkat illetve az eltelt idővel, vagy annak hatványaival arányos – szekuláris – változásokat okoznak a paraméterekben.
A pályaszámítás a gyakorlatban
A fenti elveket használó pályaszámító programrészletek és a műholdak aktualizált pályaparaméterei a www.celestrak.com webhelyről érhetők el. A webhely az adatok eléréséhez a felhasználó regisztációját kéri.