A luniszoláris precesszió periódusideje

Ha a Föld adott szögsebességgel forgó merev test, akkor igaz rá az impulzusmomentum megmaradásának törvénye:

(1)

Ha a forgó merev testre forgatónyomaték hat, akkor az impulzusmomentum megváltozása:

(2)

a kis idő alatti változás pedig:

(3)

Az impulzusmomentum megváltozásának iránya a forgatónyomaték irányába mutat. A forgatónyomaték:

(4)

Ez készteti a Föld forgástengelyét precessziós mozgásra, melynek szögsebessége:

(5)

vagyis a forgástengely kicsi elfordulása adott idő alatt. Az impulzusmomentum megváltozásának abszolútértéke:

(6)

ahol Θ=23,5°, az ekliptika és az egyenlítő síkjai által bezárt szög. (3) alapján ez:

(7)

(5) felhasználásával:

(8)

A Nap és a Hold forgatónyomatéka külön-külön vehető figyelembe. A forgatónyomaték kiszámításához közelítsük a Föld tömegvonzási potenciálját a másodrendű zonális harmonikussal:

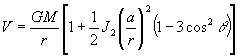(9)

Ha J₂-t a következő alakban írjuk:

(10)

úgy:

(11)

Ebből kiszámítható (itt nem részletezetten; ld. Márton, 1989) a Nap által kifejtett forgatónyomaték:

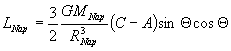(12)

A Nap átal okozott szoláris precesszió körfrekvenciája:

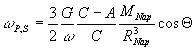(13)

ami a Föld tengelyforgásával (ω) ellentétes értelmű. A Hold forgatónyomatéka és a lunáris precesszió körfrekvenciája:

(14)

(15)

(Θ’ a Hold pályasíkja és az egyenlítő által bezárt szög.)

A luniszoláris precesszió körfrekvenciája az előző kettő összege:

= 50,37”/év (16)

amely a Föld tengelyforgásával ellentétes értelmű. Innen a luniszoláris precesszió periódusideje:

(17)

azaz T = 25 730 év

Forrás: Kis Károly: Általános geofizikai alapismeretek. ELTE Eötvös Kiadó, 2002.