GEOREFERENCIA

TÉRKÉPI VETÜLETEK ÉS GEODÉZIAI DÁTUMOK

SZABATOS HASZNÁLATA A TÉRINFORMATIKÁBAN

Elektronikus jegyzet

A ’Térképi vetületek és dátumok’, a ’Georeferencia a térinformatikában’, a ’Vetülettani alkalmazások’ és a ’Térinformatikai adatintegráció’ c. kurzusok hallgatói részére

Írta: Dr. Timár Gábor

ELTE Geofizikai és Űrtudományi Tanszék

Lektorálta:

Dr. Molnár Gábor

Budapest

2008

TARTALOM

1. Bevezetés. 3

2. A pontok síkbeli és térbeli meghatározásakor alkalmazott koordinátarendszerek.. 4

2.1 Földrajzi és ellipszoidi koodinátáknál alkalmazott mértékegységek. 4

2.2 Kezdőmeridiánok. 4

2.3 Koordinátarendszerek és kerethálózatok. 6

3. A Föld alakja és annak közelítései 7

3.1 A Föld feltételezett alakjának változása a tudományban. 7

3.2 A geoid és a forgási ellipszoid. 9

3.3 Háromszögelési hálózatok típusai, kialakításuk és a geodéziai kiegyenlítés. 10

4. Geodéziai dátumok.. 12

4.1 A háromszögelési hálózatok paraméterezése. 12

4.2 A Molodensky-féle dátumparaméterezés. 13

4.3 A Bursa-Wolf-féle dátumparaméterezés. 14

4.4 A Molodensky- és a Bursa-Wolf-féle paraméterezés összehasonlítása, gyakran előforduló hibák 16

4.5 A paraméterek megbecslése. 17

5. Térképek és vetületek.. 20

5.1 Vetületek és paraméterezésük. 20

5.2 Átszámítások különböző vetületi koordináták között 23

5.3 Helyettesítő vetületek. 24

5.4 A térképek szelvényezése és a szelvényezés által hordozott georeferencia. 26

6. Térképek georeferálása.. 27

6.1 A georeferálás és a rektifikáció. 27

6.2 A vetületi analízis és az önkényes vetületválasztás. 29

1. Bevezetés.

A térinformatikában a georeferencia annak a módszertana, hogy a térinformatikai rendszerben rögzített objektum minden pontjának megadjuk a koordinátáit és azt, hogy ezek milyen koordináta-rendszerben értendők. Ezen túlmenően leírja e koordináták más rendszerekbe történő átszámításának módját is. Az objektumok lehetnek vektorosak, ekkor a töréspontok koordinátáit kell definiálnunk, vagy raszteresek, ekkor minden egyes raszter koordinátáit meg kell tudjuk adni valamilyen leíró eljárással.

A fenti definíció első mondata kísértetiesen hasonlít a felmérési geodézia alapfeladatához. A térinformatikai alkalmazás azonban egyrészt azt feltételezi, hogy a terepi felvételezést mások már elvégezték, így a georeferencia nagyon ritka kivételektől eltekintve irodai, számítógépes munka. Ráadásul, mint arra alább kitérünk, a térinformatikában mások, alacsonyabbak a pontosságigények, mint a geodéziai alkalmazásokban. Talán ez az oka annak, hogy bár a jelen munkában ismertetett eljárások mindegyike ismert a geodéziában, az ezekkel foglalkozó szakemberek érdeklődését nem keltette fel a számukra elfogadhatatlan pontosságú alkalmazások fejlesztése. A térinformatikában mindazonáltal nagyon is lényeges a méteres vagy néhány méteres pontosságú koordináta-kezelés, bár a hazai szakirodalomban még nem jelent meg olyan tankönyv, amely e módszereket összefoglalná. A jelen munka erre tesz kísérletet.

A georeferencia azért alapvető jelentőségű a térinformatikában, mert ez a kulcsa a sokféle bemeneti adat egységes térbeli kezelésének, a térbeli adatintegrációnak. Ezzel a problémával minden térinformatikai felhasználó találkozott már, ha adatai nem csupán egyetlen koordináta-rendszerben voltak adottak. Bízom benne, hogy e könyv sokakat hozzásegít e problémák, feladatok szabatos, a saját igényeinek megfelelő pontosságú megoldásához.

Még itt, a bevezető részben szükséges, hogy meghatározzuk a térinformatikai pontosság fogalmát. Ez relatív fogalom; a GPS-gyakorlatban általában a méteres-néhány méteres (0,5-5 méter) hiba tartozik hozzá. Amennyiben pl. szkennelt térképi állományt georeferálunk, abból kell kiindulnunk, hogy a térképek előkészítése, nyomtatása, a papíranyag nyomtatás utáni száradása és a szkennelés során kb. 0,5 milliméter pontosság tartható meg. Ebből az következik, hogy a georeferencia elvárt abszolút pontossága az alkalmazott térkép vagy raszteres adatrendszer méretarányának függvénye; 1:10.000 méretarány esetén pl. 5 méter, míg 1:50.000 méretaránynál 25 méter. Fontos, hogy nem érdemes (nem költséghatékony) a 0,5 milliméteres térképi pontosságnál precízebb követelményrendszer, hiszen a bemenő információinkat ennyi hiba mindenképp terheli az esetek túlnyomó részében.

A könyv olvasása során néhány részt, kiegészítő információkat, esetleg matematikai levezetéseket kisebb betűvel, keskenyebb oldaltükörrel szedtünk. A georeferencia lépései ezek nélkül is megérthetők, ezek inkább háttérként, az elmondottak történeti vagy matematikai megértéséhez szükségesek, de a könyv ezek átugrásával is olvasható.

2. A pontok síkbeli és térbeli meghatározásakor alkalmazott koordinátarendszerek

2.1 Földrajzi és ellipszoidi koodinátáknál alkalmazott mértékegységek

Térképeinken megszokhattuk, hogy a szögeket fok-perc-másodperc rendszerben olvashatjuk le. A teljes kör 360 fok, egy fok 60 percre, egy perc pedig 60 másodpercre osztható, így tehát egy fok 3600 másodpercből áll.

A hosszúsági körök mentén az egységnyi szöghöz tartozó fizikai távolságok – a Földet gömb alakkal közelítve – gyakorlatilag azonosak. 1 fok különbség a meridián mentén kb. 40000000 m/360 fok ≈ 111111 méter. 1 másodperc ennek 3600-ad része, vagyis kb. 30,86 méter, ennyi a távolság két, egymástól 1 másodperc szögtávolságra levő paralelkör között. A szélességi körök mentén az egységnyi szöghöz tartozó távolság az adott hely szélességétől is függ, az előbbi számértékeket a szélesség koszinuszával kell normálni. Budapest 47,5 fokos földrajzi szélességén az egy hosszúsági fok szögkülönbségnek 75208 méter, egy másodperc szögkülönbségnek 20,89 méter távolság felel meg.

A fok-perc-másodperc rendszer azonban nem kizárólagos. Franciaországban, illetve volt francia gyarmatok (pl. Libanon) térképein újfok (gon, ill. grad) beosztással is találkozhatunk. A teljes kör 400 újfokból áll. 1 újfok 100 újpercet, illetve 10000 újmásodpercet tartalmaz.

A térinformatikai szoftverek sok esetben radiánban kérik különböző, ellipszoidi koordinátákhoz kötött állandók megadását. Itt hívjuk fel a figyelmet, hogy pl. a MS Excel táblázatkezelő program is radiánban értelmezi a szögfüggvények bemenő változóját. A teljes kör 2π radián, így 1 radián kb. 57,3 foknak felel meg.

Az 1870-es években az átmenetileg Németországhoz került Elzász-Lotharingiában elvégezték a francia és a német hálózat összeillesztését azonos alappontok alapján. Az illeszkedésnek 10 métert meghaladó hibája volt. Később kiderült, hogy a francia és a német hálózat alapvonalait (lásd a következő pontban) más-más méter-mérték (platinaötvözetű méterrúd) felhasználásával kalibrálták. A német (de eredetileg szintén Párizsból vásárolt) rúd hossza 13,55 mikronnal hosszabb volt. Ennek csak nagy távolságok esetén van jelentősége, de akkor annál nagyobb: több száz kilométeres távolságon összejön a 10 méteres hiba. A német méterrúd hossza lett később az ún. legálméter, amely tehát 1,00001355 nemzetközi méternek felel meg. A Bessel-1841-Namíbia ellipszoid (Namíbia német gyarmat volt) nagytengelye az eredetiének pont ennyiszerese, a legálmétert emiatt „Namíbia-méter”-ként is említik.

2.2 Kezdőmeridiánok

Míg a szélesség irányában létezik a koordinátarendszernek kitüntetett iránya, a forgástengely helyzete egyértelműen meghatározza a pólusok és az egyenlítő helyét, és a felület minden pontjának ellipszoidi szélességét. A hosszúság tekintetében nincs ilyen kitüntetett irány, ezért azt önkényesen kell megválasztanunk.

A háromszögelési hálózat kezdőpontját általában kezdő- vagy nullmeridiánnak választják (3.3. pont). A hálózat pontjainak ellipszoidi hosszúságát e délkörhöz képest adják meg. A térinformatikában azonban a dátumokat nemcsak az elhelyezésük és tájékozásuk alapján kell leírjuk, hanem nullmeridiánjaikat is le kell tudnunk írni. Ahogyan az elhelyezés és tájékozás leírásakor egy etalon-dátumot, a WGS84-et választottuk, és a többi alapfelület helyzetét ehhez képest írjuk le, ugyanúgy a kezdőmeridiánok közül is kiválasztunk egyet – legyen ez a greenwich-i délkör – és valamennyi nullmeridiánnak ehhez képest adjuk meg a hosszúságkülönbségét.

A greenwich-i délkör világszabvány voltát az 1884-ben Washingtonban megtartott Nemzetközi Meridián Konferencia (International Meridian Conference) által elfogadott 2. alapelv „javasolta a világ kormányai számára”, 22-1-es szavazati aránnyal (Haiti, akkori nevén San Domingo szavazott ellene, Franciaország és Brazília tartózkodott). Franciaország csak 1911-ben vezette be a greenwich-i meridián használatát, és számos francia térkép mind a mai napig párizsi kezdőmeridiánnal és újfokban is feltünteti a hosszúságokat.

Nem véletlen, hogy ebben az időpontban vetődött fel komolyan az egységes kezdőmeridián kérdése. A szikratávíró feltalálása és elterjedése tette ugyanis lehetővé az egyes kezdőmeridiánok közötti hosszúságkülönbség meghatározását. A szikratávírón továbbított időjel alkalmazásával lehet az ehhez szükséges egyidejű csillagászati helymeghatározást végrehajtani.

Néhány nullmeridián és a greenwich-i délkör hosszúságkülönbségét a következő táblázatban találjuk meg.

nullmeridián	hosszúságkülönbség Greenwich-hez képest
Párizs	2° 20’ 14,025”
Róma	12° 27’ 8,04”
Madrid	–3° 41’ 16,48”
Oslo	10° 43’ 22,5”
Pulkovó	30° 19’ 42,09”
Ferro^1	–17° 40’
Ferro^2	–17° 39’ 46,02”
Ferro^3	–17° 39’ 45,975”
Bécs, Stephansdom^4	34° 02’ 15”
Bécs, Stephansdom^5	16° 22’ 29”
Gellérthegy^6	36° 42’ 51,57”
Gellérthegy^7	36° 42’ 53,5733”
Gellérthegy^8	19° 03’ 07,5533”

¹Németország, Ausztria, Csehszlovákia, Jugoszlávia esetén. ²Magyarországon, ill. a Monarchiában, az ún. Albrecht-féle különbség. ³A Bureau International de l’Heure szerint. ⁴Ferrótól, az 1806-es rendszer szerint. ⁵Az Albrecht-különbség alkalmazásával. ⁶Ferrótól, az 1821-es rendszer szerint. ⁷Ferrótól, az 1909-es rendszer szerint ⁸Az 1909-es rendszer szerint, az Albrecht-különbség alkalmazásával

Amint azt a táblázatból is láthatjuk, az egyes nullmeridiánok többféle értékkel is jellemezhetők. Ez a helyzet az 1930-as éveket megelőzően Magyarországon is szinte kizárólagosan használt ferrói délkörrel kapcsolatban is. Ferro (mai nevén: El Hierro) a Kanári-szigetek legnyugatibb tagja, a ferrói délkör maga pedig „az Óvilág legnyugatibb pontjához” simul. A ferrói délkör a valóságban a párizsi nullmeridiánt jelenti, Ferro és Párizs szögkülönbsége a Bureau International de l’Heure (BIH) szerint hajszálpontosan 20 fok. Magát a ferrói kezdőmeridiánt szintén egy, ma már feledésbe ment, Richelieu francia bíboros által kezdeményezett, Párizsban megtartott nemzetközi tanácskozás javasolta egységes kezdőmeridiánnak, még a XVII. században.

A táblázatban megadott három érték közül a BIH szerinti pontosan a 20 fokos Párizs-Ferro szögtávolságot jelenti, az Albrecht-féle különbség ehhez képest kb. egy méteres eltérést jelent. Németország, és nyomában Ausztria, majd a Monarchia további két utódállama is, ezt módosítottak. Ennek az volt az oka, hogy a régi berlini csillagvizsgáló tornyának hosszúságáról kiderült, hogy hibás: az eltérés 13,39 másodpercnek adódott. Ezt az értéket hozzáadjuk a 17° 39’ 46,02”-es Albrecht-féle különbséghez, akkor 17° 39’ 59,41”-et kapunk, ami másfél méter körüli hibával 17° 40’-re kerekíthető. Ily módon a topográfiai térképek szelvénybeosztását is meg lehetett tartani.

A gellérthegyi délkör esetén azért jegyeztük meg, hogy melyik rendszerre vonatkozik az érték, mert ez is, akárcsak a geodéziai kezdőpont koordinátái, alapfelületről alapfelületre változó számadat.

Előfordul az is, pl. spanyol vagy norvég topográfiai térképeken, hogy a hosszúságok Greenwich-től számítva vannak feltüntetve, azonban a térképsorozat szelvényezése, a szelvényhatárok még a régi, esetünkben a madridi vagy az oslói délkörhöz képest értelmezett kerek hosszúságokra illeszkednek (ÁBRA).

Más égitestek (Mars, Hold, Vénusz) térképezésekor is definiáltak kezdőmeridiánokat. A Mars esetén az Airy-0 kráteren (névválasztása a greenwich-i obszervatórium korábbi igazgatója után történt), a Hold esetén pedig a látható oldal középpontjában levő Bruce-kráteren halad át a kezdőmeridián.

A kezdőmeridiánok definíciója ma már a nemzetközi égi koordinátarendszerhez illetve -kerethez (ICRF; International Celestial Reference Frame) kötött, az égitestek tengely körüli forgása paramétereinek (periódusidő, precessziós és nutációs állandók) és a tavaszpont (az ekliptika és az egyenlítő felszálló irányú metszéspontja) egy rögzített időpontbeli helyzetének alapján történik.

2.3 Koordinátarendszerek és kerethálózatok

Bármilyen objektum sík- vagy térbeli elhelyezését, elhelyezkedésének definiálását koordinátarendszerek teszik lehetővé. A koordinátarendszerekben (reference system) az objektum koordinátái (régebben használt magyar szakkifejezéssel: összrendezői) a helyet egyértelműen azonosítják. A koordinátarendszerek tengelyei emiatt egymástől lineárisan függetlenek. A térinformatikában használt rendszertípusok:

- síkbeli derékszögű koordinátarendszer (síkkoordinátarendszer);

- térbeli derékszögű koordinátarendszer;

- gömbi polárkoordináta-rendszer (gömbi koordinátarendszer);

- ellipszoidi koordinátarendszer.

Az első kettő tengelyei a síkban ill. a térben egymásra kölcsönösen merőleges egyenesek, az utóbbiakat egy középponttól (ill. a gyakorlatban valamely felszíntől, pl. magának a gömbnek vagy az ellipszoidnak a felületétől) értelmezett távolság, és két irányszög (szélesség és hosszúság) jellemzi (2.4. pont). A koordinátákat ebben a rendszerben valamely, a 2.1. pontban megadott mértékegységgel adjuk meg.

A koordinátarendszereket illetve a koordinátákat a valóságos térben szinte soha nem láthatjuk, azok látható, fizikai valóságukban nem léteznek. Emiatt a koordinátarendszereket fizikailag diszkrét pontokban létesített alappontok és azoknak az adott rendszerben meghatározott koordinátái valósítják meg. Ezt a koordinátákkal jellemzett, fizikailag is létező, észlelhető pontsokaságot kerethálózatnak vagy koordinátakeretnek (reference frame) nevezzük. Minden geodéziai alaphálózat lényegében egy kerethálózat.

A kerethálózat létrehozása szükségszerűen (elvi és/vagy mérési) hibákkal terhelt, emiatt a kerettel definiált koordinátarendszerekben mindig van egy, a keret létrehozásának technológiájából eredő bizonytalanság. A geodéziai hálózatok esetén a Föld ellipszoidtól eltérő potenciálelméleti alakja elvi hibát, míg a véges mérési pontosság mérési hibát okoz a kerethálózat létrehozásakor.

3. A Föld alakja és annak közelítései

A Föld alakjának jellemzésére többféle definíció kínálkozik. Mi ezek közül mindenképp olyant keresünk, amely függvény formájú: adott gömbi vagy ellipszoidi koordinátához egy értéket rendel: ez lehet a középpontból az adott ponthoz húzott sugár hossza vagy egy tetszőleges módon megválasztott nívófelülethez képest értelmezett magasság.

A szilárd, illetve folyadék fázisnak a légkörrel érintkező határa egy nyilvánvaló lehetőség. E meghatározással kapcsolatban azonban rögvest értelmezési problémákat találunk: a szilárd halmazállapotú növényzet része-e bolygónk alakjának? Mit kezdhetünk az épületekkel vagy az állandóan sodródó jéghegyekkel?

Még ha ezeket a kérdéseket így vagy úgy meg is válaszoljuk, egy gonddal mindenképp szembesülünk: ez a meghatározás nem eredményez egyértékű függvényt. A barlangok, a túlhajló sziklafalak esetén azonos gömbi vagy ellipszoidi koordinátákhoz több magasságérték is rendelhető. Valahogy el kell „simítanunk” a fázishatárok által definiált alakot.

A gravitációs, illetve nehézségi erőtér pontosan ilyen simított felületeket kínál. A Föld geoid (szó szerinti értelemben földszerű) alakját éppen a nehézségi erőtérnek egy bizonyos nívófelületével lehet legjobban leírni. Nívófelületből végtelen sok van: azt választjuk, amelyik a középtengerszinthez legjobban illeszkedik. Ebből következik a geoid kevésbé szabatos, ugyanakkor nagyon szemléletes definíciója: a tengerszint folytatása a szárazföldek alatt. Lássuk, hogyan alakult ki az emberiség közös ismeretanyagában ez a kép, és mire használható a helymeghatározás gyakorlatában.

3.1 A Föld feltételezett alakjának változása a tudományban.

Az antik görögök tisztában voltak a Föld gömbszerű alakjával. Eraszthotenész híres kísérlete, melyben a nyári napfordulókor, tehát azonos időpontban, különböző szélességeken a Nap sugarainak beesési szögének eltéréséből megbecsülte a Föld sugarát, közismert. A becslés pontossága az akkori technikát figyelembevéve figyelemreméltó.

Bár az európai középkor a görögöket tekintette tudományos elődeinek, a Föld alakját mégis laposnak tekintették. Ebből származtak az olyan hiedelmek, mint a „világ vége”; az arra a kérdésre adott válasz, hogy ha azonos irányban sokáig megyünk, hová is jutunk egy lapos, de végesnek tekintett felületen.

A XV.-XVI. század hajózási eredményei és felfedezései, elsősorban Magellán hajóinak Föld körüli útja (1520-21) megrendítették ezt a világképet. Bár a változást a tudományt uraló egyház csak lassan fogadta el, mégis újra teret nyert az a gondolat, hogy bolygónk gömbszerű, illetve az akkori elképzelések szerint gömb alakú.

A szabályos gömb alakot többféle megfigyelés is megkérdőjelezte. A XVII. században az időmérés pontosságát nagyban megnövelte az ingaóra. A pontosan beállított ingaórák napi 1-3 másodperc hibával tudták a Nap két delelése közötti időtartamot megmérni. Egy ilyen, jól beállított ingaórát más szélességi körre – például Párizsból a dél-amerikai Cayenne-be (Francia Guyana) – elszállítva azonban jelentős, egy percet is meghaladó hiba lépett fel. Ennek az az oka, hogy az inga lengésidejét befolyásoló nehézségi gyorsulás értéke változik a földrajzi szélességgel. Párizs közelebb van a Föld tömegközéppontjához, mint Cayenne. Eszerint a Föld gömb alakja kissé torzult, a sugara szélességfüggő, tehát az alak forgási ellipszoid.

Torzult, forgási ellipszoid, de hogyan? Elnyúlt vagy lapult? A sarki vagy az egyenlítői sugár a nagyobb? Mai ésszel talán meglepő, hogy ez a vita több évtizedig foglalkoztatta a csillagászokat, földmérőket, matematikusokat (ez a három szakma akkor szinte azonos volt, legjobbjaik az összes felsorolt szakterületen működtek). Végül a Francia Tudományos Akadémia által szervezett fokmérések oldották meg a problémát. Lappföldön, magas szélességeken, és Peruban, az Egyenlítő közelében is megmérték egy-egy meridiánív hosszát két olyan pont között, ahonnan valamely csillag delelési magassága között pontosan 1 fok különbség adódott. Egyértelmű lett a válasz: Földünk lapult, sarki sugara kisebb, mint az egyenlítői.

A lapult forgási ellipszoid a 2. fejezetben leírt módon egyértelműen definiálható két számértékkel. Ezek közül az egyik hagyományosan a fél nagytengely, tehát az egyenlítői sugár, ez megadja az ellipszoid nagyságát. A másik szám, a fél kistengely, a lapultság vagy az excentricitás definiálja az ellipszoid alakját. A korabeli szerzők általában a lapultság reciprokát, az inverz lapultságot adták meg. Ez a szám azt írja le, hogy a sarki és az egyenlítői sugár hossz-különbsége hányadrésze az egyenlítői sugárnak.

Az 1700-as évek végén, az 1800-as évek első felében rendkívül sok ellipszoidot publikáltak, mint a Föld alakjának mind jobb és jobb közelítéseit. Ezeket a közreadó tudós nevével és a közlés évszámával jellemezzük. Így pl. a Zách 1806-os ellipszoid a magyar földmérő-csillagász Zách Ferenc 1806-ban publikált ellipszoidalak-számpárosát jelenti.

Az ellipszoidok nagytengelye és inverz lapultsága nem teljesen független egymástól E két számérték időbeli változása igen érdekes. Az első időszakot a nagytengely-becslések növekedése, és az inverzlapultság-becslések csökkenése jellemezte. A Föld nagyobb és gömbszerűbb volt, mint azt az első észlelők gondolták. A nagytengely és a lapultság megállapítása azonban technikai és észlelési szempontból nem igazán bonyolult feladat. Miért hát az eltérő eredmények és miért ez a változás?

Az első észlelők egy-egy meridiánív mentén, egy adott fokmérést végezve publikálták adataikat. Az oszták Walbeck 1819-ben kiadott ellipszoidja volt az első, amely több, öt független fokmérés adatainak átlagán alapult. Viszont ha egy ellipszoidnak tartott test becsült nagytengelye és lapultsága helyről helyre változik, akkor az a test nem ellipszoid. Majnem az, de nem teljesen.

Ez a „nem teljesen”, ez kiderült a későbbiekben (3.3. pont) tárgyalandó háromszögelési hálózatok kialakításakor is. A fejezet bevezetőjében említett gravitáció-elméleti alakleírást ennek alapján Carl Friedrich Gauss definiálta az 1820-as években, majd az említett geoid nevet Johann Benedict Listing javasolta 1872-ben. A geoid ismeretében értelmezhetjük az ellipszoidparaméterek becslésében mutatkozó trendet: a geoid európai darabja alapján a Föld kisebbnek és lapultabbnak tűnik.

A ma használatos ellipszoidok (WGS84, ETRS89, stb., lásd 3.2. pont) paramétereit már a teljes Földre meghatározott geoidalak figyelembevételével határozták meg ily módon, hogy

• az ellipszoid geometriai középpontja a Föld tömegközéppontjába essen;
• az ellipszoid forgástengelye a Föld forgástengelyével egybeessen, és
• az ellipszoid és a geoid térfogata azonos legyen és
• az ellipszoid és a geoid magassági eltérése a teljes felszínt figyelembe véve minimális legyen.

Adott ponton a geoid és a (választott vagy a legjobban illeszkedő) ellipszoid felülete között a függővonal mentén mért távolságot geoid-undulációnak nevezzük. A legjobban illeszkedő WGS84 ellipszoidhoz képest a geoidunduláció-értékek a Föld felszínén a ±120 métert nem haladják meg.

Összegezve, mai ismereteink: a Föld egyenlítői sugara kb. 6378 kilométer, az egyenlítői és a sarki sugár hosszának különbsége (a gömb alak hibája) kb. 21 kilométer, az ellipszoid alak hibája pedig 120 méter.

3.2 A geoid és a forgási ellipszoid

A geoid matematikai leírása több módon lehetséges. Megadhatjuk a gömbi vagy ellipszoidi koordináták egyenközű rácshálója csomópontjaiban érvényes, a tömegközéppontból a geoidfelszínhez mutató sugárhosszakat. Megadhatjuk ugyanilyen rácshálóban a geoidfelszínnekk a legjobban illeszkedő ellipszoid felszínéhez képest értelmezett magassági helyzetét, a fent definiált geoid-undulációt. Megadhatjuk a geoidot gömbfüggvény-sorfejtéses alakban is. Helyi, illetve regionális geoid-felszíndarab leírására vetületi koordináták szerinti rácshálót is használhatunk.

Bármelyik megoldást választjuk is, az nyilvánvaló, hogy a geoid igen bonyolult felület. Amennyiben a felszínt vagy annak egy darabját térképen akarjuk ábrázolni, ehhez valamilyen térképi vetületet kell majd választanunk. A vetületi egyenletek, amelyek a gömb leképezésekor még viszonylag egyszerűek, igen bonyolulttá válnak, ha ellipszoidról kívánunk vetíteni. A geoid alapfelület ebből a szempontból matematikailag kezelhetetlen. Különösen pedig akkor számított annak, amikor a térképvetületek matematikáját kidolgozták, a XIX. században, amikor nem állt rendelkezésre számítógép. Emiatt a térképészeti és geodéziai alkalmazásokban a geoidot forgási ellipszoiddal helyettesítjük.

név	a	b	1/f	f	e	e2
Laplace 1802	6376615	6355776.4	306.0058	0.003268	0.08078	0.00653
Bohnenberger 1809	6376480	6356799.51	324	0.003086	0.07851	0.00616
Zach 1809	6376480	6355910.71	310	0.003226	0.08026	0.00644
Zach-Oriani 1810	6376130	6355562.26	310	0.003226	0.08026	0.00644
Walbeck 1820	6376896	6355834.85	302.78	0.003303	0.08121	0.00659
Everest 1830	6377276	6356075.4	300.8	0.003324	0.08147	0.00664
Bessel 1840	6377397	6356078.96	299.1528	0.003343	0.08170	0.00667
Struve 1860	6378298	6356657.14	294.73	0.003393	0.08231	0.00677
Clarke 1866	6378206	6356583.8	294.98	0.00339	0.08227	0.00677
Clarke 1880	6378249	6356514.87	293.465	0.003408	0.08248	0.00680
Hayford (Int'l) 1924	6378388	6356911.95	297	0.003367	0.08199	0.00672
Krassovsky 1940	6378245	6356863.02	298.3	0.003352	0.08181	0.00669
GRS67	6378160	6356774.52	298.2472	0.003353	0.08182	0.00669
GRS80	6378137	6356752.31	298.2572	0.003353	0.08182	0.00669
WGS84	6378137	6356752.31	298.2572	0.003353	0.08182	0.00669
Mars (MOLA)	3396200	3376200	169.81	0.005889	0.10837	0.01174

2. táblázat. A térképészetben használatos ellipszoidok adatai.

A közelítéshez használt ellipszoid a legtöbb esetben valamely előre definiált, jól ismert paraméterekkel rendelkező alapfelület (1. táblázat). Figyeljük meg, hogy az egyes ellipszoidok nagytengelyei között, bár a név és az évszám azonos, különféle verziók is lehetségesek (pl. az Everest-ellipszoidok, Bessel 1841-ellipszoid). Ennek az az oka, hogy ezen az alapfelületek nagytengelyeit nem metrikus rendszerben, hanem pl. yardban vagy lábban adták meg. Ebben az esetben a metrikus rendszerre való áttéréskor fontos az adott hosszmérték és a méter közötti váltószám. Nem mindegy, hogy ezt a váltószámot hány tizedesjegyig definiálják: a negyedik tizedesjegy elhagyása a yard-méter átváltásnál a köznapi életben nem okoz problémát, de ha ebből a yardból több millió van (mint a földsugár esetében) az eltérés több száz méteres! Ha lehet, ennél is érdekesebb a Bessel-1841 ellipszoid esete. Ezt méterben definiálták, mégis több változata van, az nemzetközi és legálméter közötti, az előző fejezetben említett eltérésnek megfelelően.

Az ellipszoidnak a geoidhoz való illesztése a geodézia egyik fontos feladata. A kozmikus geodézia eszközeinek megjelenéséig ez a gyakorlatban a háromszögelési hálózatok kialakításával és (később) kiegyenlítésével történt.

3.3 Háromszögelési hálózatok típusai, kialakításuk és a geodéziai kiegyenlítés

Két pont távolságának meghatározása – amennyiben a pontok nincsenek túl messze egymástól – a pontok közötti egyenesen a hosszmértéknek megfelelő egység egymás mögé fektetésével lehetséges. Amennyiben a két pont távolsága nagyobb, ez az eljárás hirtelen igen bonyolulttá és nehezen kivitelezhetővé válik. Egymástól több száz méter távolságban lévő pontok távolsága ilyen módon már nagyon munka- és költségigényes.

Már a XVII. század elején kifejlesztették azt a módszert, amellyel a nagyobb távolságok megmérése visszavezethető egy kisebb távolság és több-kevesebb szög megmérésére. 1615-ben a holland Snellius végezte el az első háromszögelést, amellyel két város, az egymástól elég messze eső Alkmaar és Breda templomtornyai közötti távolságot mérte meg. A mérés során a két város között elhelyezkedő templomtornyokra, mint csúcspontokra háromszöghálót létesített, és a háromszögek szögeit megmérte. Ezek után csak egy oldalhosszt hagyományos módon megmérve a háromszögháló valamennyi oldalhossza kiszámítható.

Snellius mérése egy érdekes felfedezéshez járult hozzá: a háromszögek mért szögeinek összege nem 180°-nak, hanem annál kicsivel többnek adódott. Ez a Föld gömbszerű (nem sík) alakjának következménye, a gömbfelületen értelmezett háromszögekre igaz ez. A geometria új ága, a gömbháromszögtan születésének ez volt a pillanata.

A háromszögelési hálózatokkal nemcsak távolságok, hanem koordináták is meghatározhatók. Ehhez az szükséges, hogy a hálózat egy pontjának meghatározzuk a földrajzi koordinátáit. Ezért van az, hogy a háromszögelési hálózatok főalappontjának általában egy csillagvizsgálót választottak: a helymeghatározás itt a legegyszerűbb. A hálózat szükséges része még az ún. alapvonal: két, a hálózatba kapcsolt pont, amelynek távolságát hagyományos módon nagyon pontosan megmérik. Amennyiben ezek adottak, a háromszögelési hálózat csomópontjainak magasságát szintezéssel megmérik, a köztük fellépő szögeket meghatározzák, úgy – itt nem részletezett módon – valamennyi alappont földrajzi koordinátája megbecsülhető egy előre kiválasztott ellipszoidot feltételezve. A kapott koordinátákban a földrajzi hosszúság a csillagvizsgáló délköréhez – meridiánjához – képest értelmezett szögkülönbség lesz.

Ez utóbbi megállapítás a magyarázata annak, miért ismeretes olyan sok kezdőmeridián a XVIII. és XIX. századi geodéziai felmérésekben: a szikratávíró feltalálása előtt nagyon körülményes feladat volt két távoli csillagvizsgáló hosszúságkülönbségét pontosan meghatározni. A közös háromszögelési hálózatba kapcsolás nem volt mindig megoldható – és mint azt mindjárt látni fogjuk, az sem vezetett volna teljesen pontos eredményre. Emiatt rendkívül változatos, és sokszor igen szellemes módokat találtak arra, hogyan is mérhetik meg valamely csillag pozícióját a két obszervatóriumban pontosan ugyanabban a pillanatban. A Jupiter-holdak fogyatkozásai, illetve más esetekben az obszervatóriumok közötti hegytetőkön végzett lőpor-robbantások is eszközül szolgáltak. A greenwich-i kezdőmeridián csak a XX. század első felében kezdett általános szabvánnyá válni és még ma sem kizárólagos (lásd 2.2. pont).

Az egyes alapponti koordináták meghatározásának ellenőrzéseként a háromszögelési hálózatokba több alapvonalat is bekapcsoltak, illetve – ami az eljárást forradalmasította – több alapponton (az ún. Laplace-pontokon) is meghatározták a földrajzi koordinátákat, csillagászati eszközökkel. Az így mért helyzet azonban eltért a más mérések alapján a háromszögháló felhasználásával számított helyzettől. Az eltérés mindig jelentkezett és nem volt előre jósolható. Az eltérés oka a Föld ellipszoidtól eltérő, geoid alakja. Az egyes pontokon végzett csillagászati helymeghatározás a helyi vízszintes és függőleges irány ismeretén alapul, ezek az irányok azonban az ellipszoidról eltérő alak miatt helyről helyre kismértékben változnak.

A probléma a XIX. század első felében akkora jelentőségű volt, hogy Carl Friedrich Gauss éppen ennek a megoldására fejlesztette ki a legkisebb négyzetek módszerét. A cél az, hogy az alappontok koordinátáit úgy változtassuk meg, hogy a Laplace-pontokon fellépő eltérések négyzetösszege minimális legyen. Az eljárás neve: a geodéziai hálózat kiegyenlítése, lényegében a geoid alak okozta hibák egyenletes elosztása, „elkenése” a hálózat területén. A kiegyenlítés eredménye: a terepen állandósított alappontok és azok rögzített, „kőbe vésett” koordinátái.

Mit eredményez a kiegyenlítés, mármint geometriai szempontból? Egy olyan ellipszoidot, amelynek méretparamétereit a hálózati feldolgozás elején rögzítettük, amelynek kistengelye (közel) párhuzamos a Föld forgástengelyével, és amely térben a legjobban illeszkedik a geoidnak ahhoz a darabjához, amelyre a kiegyenlített háromszögelési hálózat kiterjed. Ennek az ellipszoidnak a középpontja nem esik egybe a Föld tömegközéppontjával. Ily módon az ellipszoidnak már nemcsak a méretparaméterei ismertek, de a térbeli elhelyezése is adott.

A térbeli elhelyezés és annak módja szempontjából három típust különítünk el:

Önkényes elhelyezés: csak egy csillagászati alappont van, a hálózat nincs kiegyenlítve, az ellipszoid térbeli helyzete a geoid egy pontjának normálisához rögzített. Jellemzően a kis óceáni szigetek önálló geodéziai rendszerei ilyenek, sokszor ASTRO megjelöléssel. A korai, de geodéziai alappal már rendelkező térképművek alapfelülete sok esetben ilyen.

Relatív elhelyezés: a háromszögelési hálózat kiegyenlítése megtörtént, annak eredményeként az ellipszoid térbeli helyzete a geoid egy felületdarabjához képest optimális.

Abszolút elhelyezés (földi ellipszoid): az alapfelület geometriai középpontja a tömegközéppontban van, kistengelye a forgástengellyel egybeesik. Hagyományos, földi geodéziai-geofizikai eszközökkel nem valósítható meg (felszíni mérésekkel a tömegközéppont iránya nem határozható meg), definiálásához műholdas geodéziai eszközök (Doppler-mérések, GPS) szükségesek, az 1960-as éveket megelőzően földi ellipszoidokat nem definiáltak.

4. Geodéziai dátumok

A geodéziai alapfelület, idegen szóval dátum, az ellipszoid méretére és alakjára vonatkozó adatok, kiegészítve az ellipszoid elhelyezésével és esetlegesen a tájékozásával kapcsolatos paraméterekkel. Ez az adatsor többféleképpen megadható. Az alábbiakban ezeket a lehetőségeket mutatom be.

Elöljáróban nagyon fontos megjegyezni, hogy mivel a különböző dátumok ellipszoidjának mérete, elhelyezése és tájékozása különböző, ezért a különböző dátumokon értelmezett (különböző háromszögelési vagy más hálózatokon alapuló) alapponti és terepi koordináták eltérőek. Egy konkrét tereppont ellipszoidi koordinátái más-más dátumokon értelmezve különbözők! A térinformatikai rendszerek képesek arra, hogy ezek között átszámításokat végezzenek, ha az érintett dátum kezeléséhez szükséges adatokat ismerik. E fejezet az ismeretükhöz szükséges paramétereket és azok meghatározásának lehetőségeit írja le.

4.1 A háromszögelési hálózatok paraméterezése

Amint az előző fejezetben bemutattam, a háromszögelési hálózatok a terepen állandósított alappontokkal és azok koordinátáival jellemezhetők. A háromszögelési hálózat is geodéziai dátum. Ahhoz, hogy térinformatikai rendszerbe illesszük, tudnunk kell, hogy milyen módon lehet a sok alappont adatait tömörebb formában, ugyanakkor mégis a teljes hálózatra jellemzően megadni, illetve azt is, hogy a térinformatikai rendszerek milyen adatokkal tudják definiálni az egyes dátumokat.

A geodéziai gyakorlatban a legelterjedtebb leírási mód az, hogy az ellipszoid méretparaméterei mellett megadják a háromszögelési hálózat egyik kitüntetett pontjának

• ellipszoidi koordinátáit;
• csillagászati koordinátáit, ill.
• az onnan kiinduló egyik háromszögoldal ellipszoidi és csillagászati azimutját.

Minthogy a kiegyenlítés az ellipszoidnak a geoidfelülethez történő simítását jelenti, ezért általában a kitüntetett ponton a geoid-unduláció nullának tekinthető. Ha bármilyen okból nem annyi, akkor annak az értékét is meg szokták adni.

A magyarországi 1972-es kiegyenlítés (Hungarian Datum 1972) geodéziai kezdőpontja a Szőlőhegy elsőrendű alappont. A dátumot úgy definiálták, hogy itt az ellipszoid 6,56 méterrel a geoid alatt van. Egy korábbi hálózatban ezen az alapponton ilyen undulációérték adódott (a Kraszovszkij-ellipszoidnak a Varsói Szerződés területéhez „simított” dátumának az itteni undulációja) és a dátumot egyéb megfontolásból ehhez kötötték. Ezt az értéket tehát a dátum definíciójakor meg kell adni, különben függőleges értelemben elhelyezési hibát vétünk.

Ez lényegesen kevesebb információ, mint a pontok koordináta-adatainak összessége. Feltételezzük, hogy ehhez a ponthoz illesztve az adott méretű és alakú ellipszoidot, az alapponti koordináták pontosan kiszámíthatók. Ez természetesen nem igaz, a hálózat, a dátum minőségét nagymértékben jellemzi, hogy ezek a koordináták milyen pontossággal rekonstruálhatók a fenti, redukált adatsor alapján. Az így adódó átlagos hiba Magyarország-méretű területen, XIX. század végi hálózatoknál 2-3 méter, XX. század közepi hálózatoknál 1,5-2 méter, modern dátumoknál fél méter körüli.

A térinformatikai rendszerek (GIS) számára azonban a fenti adatok nem megfelelő formátumúak, ráadásul ezek a programok más filozófiát is követnek a dátumok definiálásakor. A GIS programok egyik igen fontos feladata, hogy képesek átszámításokat végezni az egyes dátumokon értelmezett koordináták között. Ehhez ismerniük kell az érintett dátumok között értelmezett elhelyezése és tájékozása közötti különbségeket. A gyakorlatban a legtöbb térinformatikai szoftver ezt úgy oldja meg, hogy kijelöl egy kitüntetett dátumot (praktikusan a WGS84-et), és minden általa ismert dátum paramétereit ehhez képest tárolja. Ily módon meg kell adni az egyes dátumok ellipszoid-középpontjainak a tömegközépponthoz képest értelmezett térbeli helyzetét és esetleg a kitüntetett irányokhoz képest értelmezett elforgatását.

4.2 A Molodensky-féle dátumparaméterezés

Két geodéziai dátum közötti kapcsolat megadásának legegyszerűbb módja az, hogy csak a két ellipszoid középpontját összekötő vektort adjuk meg. A vektort a 2. fejezetben ismertetett, geocentrikus derékszögű koordinátarendszerben értelmezett komponenseivel, méterben kell megadni. Nyilvánvaló, hogy amennyiben a két dátum középpontja azonos (például mindkettő tümegközépponti elhelyezésű), akkor a kapcsolatot a nullvektor írja le, amelynek komponensei: (0,0,0). Meg kell jegyeznünk, hogy a nemzetközi, és ennek nyomán a hazai szakirodalom is a Molodensky, illetve Molodensky-Badekas-féle paraméterezés néven említi ezt az igen egyszerű leírási formát, annak ellenére, hogy a Mihail Szergejevics Mologyenszkij által leírt eredeti dátumtranszformációs formulák ennél bonyolultabbak.

A Molodensky-féle leírás három paramétere: dX, dY és dZ, méterben adott távolságok írják le a vizsgált dátumellipszoidok geometriai középpontjainak egymáshoz képest értelmezett helyzetét. Ha a céldátum a WGS84 földi alapfelület, úgy a kiinduló dátum dX, dY és dZ paraméterei az ellipszoidnak a földi tömegközépponthoz viszonyított helyzetét adják meg. Amennyiben egy alappont derékszögű koordinátait ismerjük az egyik (1.) dátumon, a paraméterek segítségével a második (2.), ún. céldátumon értelmezett geocentrikus koordináták a következő egyszerű összefüggéssel megkaphatók:

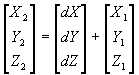(4.2.1)

A kiinduló és a céldátumon értelmezett ellipszoidi koordináták közötti szögkülönbség a geocentrikus koordinátákra történő át- és azokról való visszaszámítás nélkül is elvégezhető az ún. Molodensky-féle áthidaló formulák segítségével:

(4.2.2)

(4.2.3)

(4.2.4)

ahol 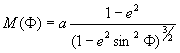a meridiángörbületi sugár; a harántgörbületi sugár; ΔΦ” és ΔΛ” a kiinduló és a céldátumon értelmezett szélesség- és hosszúságkülönbség szögmásodpercben; Δh az ellipszoid feletti magasságok különbsége; a és f a kiinduló dátumellipszoid fél-nagytengelye és lapultsága; da és df pedig ezek különbsége a kiinduló- és a céldátum között. Ha az ellipszoidi magasságok nem adottak, megbecsülhetjük őket helyi vagy globális geoidmodellek felhasználásával, vagy a (4.2.4) egyenletet el is hagyhatjuk a számításnál.

Min korábban láthattuk, a térinformatikai programok az egyes dátumokat általában egy közös vonatkoztatási rendszerhez, a WGS84 dátumhoz képest definiálják, így hidalják át azt a problémát, hogy az egyes dátumok egyszerűen leírható eszközökkel önmagukban nem, csak más dátumokhoz képest definiálhatók. Amennyiben két független dátum és a WGS84 közötti paraméterek adottak, a két dátum közötti közvetlen Molodensky-transzformáció paraméterei a linearitás következtében egyszerűen megadhatók. Legyen az A transzformáció az 1. dátum és a WGS84 közötti, a B pedig a 2. dátum és a WGS84 közötti. C-vel jelöljük az 1. és 2. dátum közötti közvetlen transzformációt. Ennek paraméterei:

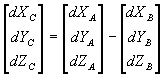(4.2.5)

függetlenül attól, hogy az 1. és 2. dátum mely ellipszoid egy-egy realizációja.

Példa: Az osztrák MGI dátum és a WGS84 közötti eltolási paraméterek: dX=+592 m; dY=+80 m; dZ=+460. A német DHDN dátum és a WGS84 közötti eltolási paraméterek: dX=+631 m; dY=+23 m; dZ=+451. Mindkét dátum a Bessel 1841-ellipsziod különféle elhelyezésű realizációja, de ennek az közvetlen paraméterek kiszámításakor nincs jelentősége. Az eredő, az MGI és a DHDN közötti közvetlen transzformáció eltolási paraméterei: dX=–39 m; dY=+57 m; dZ=+9 m.

A szakirodalomban több esetben igencsak eltérő számharmasokat találunk egy-egy alapfelület és a WGS84 dátum közötti transzformáció Molodensky-paramétereiként. Bár ez a térbeli elhelyezés pontos leírása szempontjából nyilvánvaló hibára utal, vízszintes értelemben az eltérés nem feltétlenül nagy ezek között. Két, különböző számhármassal, mint Molodensky-paraméterekkel jellemzett dátum esetében, amint azt mindjárt látni fogjuk, mindig van olyan ellipszoidi pont, amelyre nézve a két transzformáció azonos vízszintes eltolást jelent. A kérdés mindig az, hogy ez a pont az adott dátum érvényességi területére (és lehetőleg annak közepére) esik-e. Amennyiben igen, akkor mindkét paramétersor használható, és az is eldönthető, hogy ebben a pontban függőleges értelemben mennyi az eltérés. A különbség általában a geoid-unduláció figyelmen kívül hagyásából származik.

Jelölje r₁ a WGS84 ellipszoid geometriai középpontjától az 1. dátum középpontjába húzott, r₂ pedig a jelöljük a WGS84 középpontjától a 2. dátum középpontjába húzott helyvektort. Képezzük a két helyvektor háromdimenziós különbségét:

r_diff = r₁-r₂ (4.2.6)

Lássuk hogy, ez a helyvektor a középpontból az alapfelület milyen szélességgel és hosszúsággal megadott pontjára mutat:

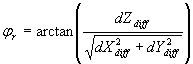(4.2.7)

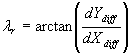(4.2.8)

míg a különbségvektor hossza (a háromdimenziós eltérés, méterben):

(4.2.9)

Amennyiben a (φ_r,λ_r) pont a dátum érvényességi területén van, úgy mindkét paramétersor alkalmazható. Ebben az esetben a különbségvektor hossza általában az ezen a ponton érvényes, a WGS84 ellipszoidhoz képest értelmezett geoidunduláció-érték körül adódik (lásd 4.6. pont), vagyis az egyik paraméterhármas nem veszi figyelembe a dátumellipszoid térbeli helyzetét. Ha a (φ_r,λ_r) pont a Föld felszínén másutt helyezkedik el, akkor valamelyik paramétersor hibás.

4.3 A Bursa-Wolf-féle dátumparaméterezés

A Bursa-Wolf-féle paraméterezés (a cseh Milan Burša és a német Helmut Wolf munkája nyomán) annyiban tér el az előző pontban tárgyalttól, hogy figyelembe veszi a két alapfelület közötti tájékozási eltéréseket, illetve az, ha a két alapfelület mérete az ellipszoidok méretéhez képest kismértékben más eltérést mutat. A transzformáció bemenő és kimenő adatai a pont derékszögű koordinátái:

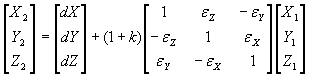(4.3.1)

A (4.3.1) képlet úgy származtatható, hogy a három irány szerinti elforgatási mátrix szorzataként előálló általános elforgatási mátrix (az ún. térbeli Helmert-transzformáció mátrix) elemeiben elvégezzük a nagyon kis (néhány, vagy maximum néhány tíz szögmásodperces) szögelfordulás esetében megtehető elhanyagolásokat és behelyettesítéseket.

A (4.3.1) egyenletben megadott elforgatási mátix nem diagonális elemeinek előjel-konvenciója kétféle lehet. Amennyiben a mátrixot a (4.3.1) egyenletben adott módon írjuk fel, az a „koordinátarendszer elforgatása” (coordinate frame rotation) konvenciónak felel meg, ekkor ugyanis a kiinduló alapfelülethez rögzített koordinátarendszert forgatjuk el a felsorolt kis szögértékekkel. Amennyiben a mátrix nem diagonális elemeinek előjelét megfordítjuk, az ún. „helyvektor elforgatása” (position vector rotation) konvenciónak megfelelő leíráshoz jutunk. Ebben az esetben a kiinduló alapfelülethez képest megadott, a vizsgált ponthoz mutató helyvektor elforgatásának komponenseit adjuk meg.

A két említett konvenció közül nincs kiválasztott szabvány. Az Egyesült Államok, Kanada és Ausztrália a „koordinátarendszer elforgatása” konvenciót, míg a nyugat-európai országok inkább a „helyvektor elforgatása” konvenciót preferálják. Az ISO19990 szabványtervezet (draft) is ez utóbbit ajánlja, azonban az USA ellenállása miatt ennek szabványkénti elfogadása belátható időn belül kétséges. Mivel a térinformatikai szoftverek többségét az Egyesült Államok - Kanada - Ausztália országcsoportban készítik, e programcsomagokban az ennek megfelelő konvenció az alapértelmezés.

Amennyiben a Bursa-Wolf paraméterezésnek megfelelő paramétercsoporthoz jutunk, feltétlenül meg kell tudnunk, hogy az melyik konvenció szerint van értelmezve. Ha ez nem tudható meg, akkor először értelmezzük a „koordinátarendszer elforgatása” módszer szerint, végezzünk ellenőrzést a saját adatainkon, és ha a transzformáció hibásnak bizonyul, fordítsuk meg a forgatási mátrix nem diagonális elemeinek előjelét.

Az előző fejezetben, a Molodensky-paraméterek esetében bemutatott, az egymás utáni transzformációk paramétereinek összegzéssel való meghatározhatósága, az ún. linearitás a Bursa-Wolf transzformációra is igaz. Ez az első pillantásra talán meglepő állítás matematikailag egyszerűen belátható. Az alábbiakban az érdeklődők számára bemutatjuk, hogy két Bursa-Wolf-dátumtranszformáció egymás utáni elvégzése hogyan és milyen pontossággal helyettesíthető egyetlen átalakítással, és e helyettesítő transzformációnak melyek a paraméterei.

A (4.3.1) egyenlet két transzformáció egymás utáni alkalmazása esetén:

x’=dx₂+(1+k₂)A₂[dx₁+(1+k₁)A₁x] (4.3.2)

alakban írható fel, ahol dx₁ és dx₂ a két eltolási vektor, k₁ és k₂ a két méretaránytényező, A₁ és A₂ a két forgatási mátrix, x a transzformáció bemenő geocentrikus helyvektora, x’ az eredmény. Az egyenlet átrendezve:

x’=dx₂+(1+k₂)A₂dx₁+(1+k₂)(1+k₁)A₁A₂x (4.3.3)

alakra hozható, innen pedig az “eredő” transzformáció dx_e,k_e és A_e paraméterei:

dx_e=dx₂+(1+k₂)A₂dx₁ (4.3.4)

k_e=k₁+k₂+k₁k₂ ≈ k₁+k₂ (4.3.5)

A_e=A₁A₂ ≈ A₁+A₂ (4.3.6)

Az (4.3.5) egyenlet végén írt közelítés azonnal, a (4.3.6) egyenletben írt pedig a mátrixszorzás elvégzésével megérthető, ha elhagyjuk a méretaránytényező, illetve az igen kis elforgatási szögek négyzetének nagyságrendjébe eső tagokat. A (4.3.4) egyenlet jobb oldalán levő összeg megfelel a második transzformációnak a dx₁ eltolásvektorra alkalmazásakor előálló eredménynek. A milliomod nagyságrendű méretaránytényező elhagyásával

dx_e=dx₂+A₂dx₁ ≈ dx₁+dx₂ (4.3.7) alakban írható. Az így kapott közelítés a transzformációkba általában behelyettesítetthez képest igen rövid vektorra alkalmazás esetén helytálló – az egyszerűsítésből származó eltérés maximum centiméteres nagyságrendű, az ezáltal okozott horizontális hiba pedig ennél is kisebb. Az eredő transzformáció paraméterei tehát valóban előállíthatóak a két egymás után alkalmazott transzformáció megfelelő paramétereinek összegeként.

4.4 A Molodensky- és a Bursa-Wolf-féle paraméterezés összehasonlítása, gyakran előforduló hibák

A Molodensky-féle (MB) és a Bursa-Wolf-féle (BW) paraméterezés közötti legfontosabb különbségek a következők:

Molodensky-paraméterezés	Bursa-Wolf-paraméterezés
egyszerűbb	bonyolultabb
általában pontatlanabb	általában pontosabb
paraméterei könnyen számíthatók	paramétereinek becslése nehezebb
a paraméterek jelentése egyértelmű	az elforgatási paraméterek kétfajta konvenciót követhetnek
minden térinformatikai szoftver ismeri	számos (de nem minden) térinformatikai szoftver ismeri

Itt jegyezzük meg, hogy az Egyesült Államok térképészeti hatósága, az NMA (National Mapping Agency), és elődei (NIMA: National Imagery and Mapping Agency; DMA: Defense Mapping Agency) a Molodensky-féle paraméterezést, míg a NATO a Bursa-Wolf-féle paraméterezést tartja követendőnek.

Bármely paraméterezést választjuk, az alapfelületek közötti átszámításnak (az egyes alapfelületek kiegyenlítési hibái miatt) a hibája csak igen kis területen elégíti ki a geodéziai számítási pontosságot, tehát marad a hiba néhány centiméteren belül. A nagy pontosságú átszámítási feladatokat más eljárással, a gyakorlatban általában magasabbfokú polinomiális illesztéssel kell megoldani. A térinformatikai szoftverek ugyanakkor csak a legritkább esetben engedik meg a felhasználónak, hogy ilyen polinomsorokat definiáljon. A térinformatikai pontosságot (ami kb. a térképi leolvasás hibájának felel meg, és topográfiai térképek esetén 5-10 méter körüli) azonban bármelyik paraméterezésnen alapuló eljárás kielégíti. Az alábbiakban megadjuk az egyes térképi felmérések alapfelülete és a WGS84 közötti átváltás jellemző országos pontosságát Magyarország mai területére, a kétfajta paraméterezés alkalmazásával.

felmérés	MB átlagos (max.) hibája	BW átlagos (max.) hibája
II. katonai felmérés	30 (200)	nem definiált transzformáció
III. felmérés-sztereo rendszer	5 (12)	1,5 (4)
DHG (1943)	2 (5)	2 (5)
EOV (1972)	1	0,2 (0,5)
katonai Gauss-Krüger (1983)	1	0,2 (0,4)

A kétféle rendszer alkalmazásakor elkövethető legnyilvánvalóbb hiba az, hogy a MB- és BW-paraméterek között az esetek túlnyomó részében nem lehet egyszerűen átszámítani. Ha ismerjük a transzformáció 7 BW-paraméterét, akkor abból nem származtatható a MB-transzformáció 3 paramétere a 3 elforgatási és egy méretarány-tag egyszerű elhagyásával!

Az a hiba is előfordul, hogy egy nem kellően pontos BW-paramétersort úgy próbálnak javítani, hogy eltolási tagjait egy másik transzformációból, vagy egy MB-parmétersorból egyszerűen kimásolják. Ezt így nem szabad csinálni, a BW-paraméterek meghatározása csak egységes algoritmussal történhet, a következő pontban leírtaknak megfelelően.

Amennyiben egy paramétersor pontatlan eredményt szolgáltat (különösen, ha az átváltási hiba kétszerese a dátumtranszformáció nélküli eltolásnak), próbálkozzunk a paraméterek előjelének (mindegyiknek) a megfordításával.

Ha így sem jutunk pontosabb átszámítási eredményekhez, akkor a BW-eljárás esetén fordítsuk meg csak az elforgatási tagok előjelét. Ellenőrizzük, hogy az elforgatási tagok mértékegysége egyezik-e a szoftver által igényelttel (szögmásodpercben vagy radiánban adottak-e az értékek). Van, ahol a méretaránytényezőt ppm-ben (part per million; milliomodrész) kell megadni, és akad olyan szoftver, ahol a tényleges arányt, egy 1-hez igen közeli tört számot kell megadni (a „nincs méretarány-különbség” számértéke az előbbi esetben nulla, az utóbbiban pedig 1). Végezetül: sok térinformatikai rendszer csak úgy „vesz tudomást” az adatfile-jaiban manuálisan módosított paraméterekről, ha újraindítjuk a programot.

4.5 A paraméterek megbecslése

Ha adott geodéziai olyan alappontok egy halmaza, amelyeknek ellipszoidi koordinátái két függetlenül meghatározott (kiegyenlített) alapfelületen is ismertek (közös alappontok), akkor meghatározhatjuk a két alapfelület (dátum) közötti Molodensky-, illetve Bursa-Wolf-paramétereket.

A Molodensky-paraméterek, tehát a két dátumellipszoid középpontja közötti vektor komponenseinek megbecslése viszonylag egyszerű, és már abban az esetben is végrehajtható, ha csak egyetlen pont, például a hálózat kezdőpontja ellipszoidi koordinátái ismertek. Ebben az esetben a koordináták, az ellipszoidok méretparaméterei és az (ismert vagy becsült) geoidunduláció-értékek felhasználásával kiszámítjuk a pont derékszögű koordinátáit mindkét rendszerben. Ezután e két koordinátahármast a pont két rendszerbeli helyvektoraként értelmezve, ezek különbségvektorának komponensei adják a keresett paramétereket. Először a kezdőponti koordinátákat a

(4.5.1)

egyenletekkel geocentrikus derékszögű koordinátákká alakítottuk először a vizsgált dátumon, majd a WGS84 ellipszoidon, majd a paraméterek

(4.5.2)

különbségek képzésével kaphatók meg.

Itt hívjuk fel a figyelmet arra, hogy a (4.5.1) képletben a h magasság az ellipszoid feletti magasságot jelenti (vö. 3. fejezet). Amennyiben az alappont tengerszint feletti magassága nem ismert, az eljárás a következő: a jellemzendő dátumon a h magasságot az ott az adott dátumellipszoidhoz képest értelmezett geoidunduláció-értékre állítjuk. Amennyiben erről nincs adatunk, válasszunk zérus értéket. A WGS84 feletti magasságértéket helyettesítsük a ponton érvényes, a WGS84-hez képest érvényes geoidunduláció-értékkel, amelyet lokális vagy globális geoidmodellből, pl. az EGM96 modellből könnyen megkaphatjuk. Az EGM96 modell és az undulációt kiszámító program az Interneten elérhető.

Amennyiben több közös alappontunk van, úgy a fenti műveletet pontonként is elvégezhetjük, és a végeredményként megadott paramétereket a pontonként meghatározott paraméterek átlagaként adhatjuk meg.

A fenti számítással olyan paramétereket kapunk, amelyek a transzformációt térben optimalizálva írják le. Arra is van lehetőség (bár lényegesen bonyolultabb számításokat igényel), hogy azt a paraméterhármast határozzuk meg, amely vízszintes értelemben minimális hibával írja le a transzformációt. A szükséges számítások elérhetőségét a fejezet végi irodalomjegyzékben találhatjuk meg.

A Bursa-Wolf transzformáció paramétereinek meghatározása lényegesen bonyolultabb feladat. A megadott levezetés áttanulmányozása és megértése csak az ezzel a problémával közvetlenül foglalkozó felhasználók számára szükséges, a többiek elegendő ha elfogadják, hogy a paraméterek megbecslése így is lehetséges. A továbbiakban egy ennél egyszerűbb módszert is láthatunk.

A legkisebb négyzetek módszerével megkapott paraméterek – az együttes becslés következtében – egyenként ritkán hordoznak információt a hálózatok közötti valódi elhelyezési viszonyokról. Általánosságban is elmondható, hogy nagyon különbözőnek látszó paramétersorok is hasonló pontossággal írhatják le két alapfelület egymáshoz képest érvényes helyzetét, és nem ismerünk olyan eljárást, amely a Molodensky-transzformációhoz hasonlóan, egyszerűen kimutatja két paramétersor ekvivalenciáját. Létezik azonban olyan eljárás, amellyel a transzformáció 3 elhelyezési, 3 tájékozási és egy skálaparamétere egymástól függetlenül megbecsülhető, pusztán a hálózatokkal kapcsolatos néhány alapinformáció segítségével.

Tételezzük fel, hogy egyik alapfelületünk a WGS84 geocentrikus dátum, míg a másik valamelyik regionális háromszögelési hálózat, amelynek adott a kezdőpontja (amelynek koordinátáját ismerjük), és adottak e pont WGS84 ellipszoidi koordinátái is. Első lépésben a (4.5.2) képletnek megfelelően kiszámítjuk a két rendszer közötti Molodensky-paramétereket, majd ezekhez az alábbiak szerint úgy választjuk meg a további 3+1 paramétert, hogy a horizontális, illetve a térbeli transzformáció pontosságát ezzel a lehető legnagyobb mértékben javítsuk.

Ehhez először is fel kell használnunk azt, hogy a skálatényező változtatása a horizontális koordinátákra gyakorlatilag elhanyagolható. A vízszintes illeszkedést az elforgatási paraméterek befolyásolják, míg a skálatényező ettől függetlenül más mennyiséghez, a geoid-undulációhoz kapcsolódik.

Észre kell vegyük továbbá, hogy a három elforgatási paraméter (r_X, r_Y, r_Z), illetve a regionális rendszer kezdőponti koordinátái (φ,λ) és a kezdőpont körüli elforgatás α szöge (3 adat) között egyértelmű megfeleltetés létesíthető a következő módon:

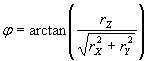(4.5.3)

(4.5.4)

(4.5.5)

illetve az inverz irányban, ellipszoidi esetben:

(4.5.6)

(4.5.7)

(4.5.8)

Ezen adatok közül a kezdőpont koordinátáit ismerjük. A kezdőpont körüli elforgatás szögére vonatkozóan csak akkor tehetünk számításon alapuló becslést, ha mind a kezdőpontnak, mind pedig a tájékozáshoz használt másik alappontnak (tehát a megadott azimuttal rendelkező háromszögoldal, mindkét végpontjának ismerjük mindkét rendszerben a koordinátáit. Ha nem is ez a helyzet, a problémát akkor is visszavezettük egy egydimenziós minimumkeresési problémára: az ismert alappont körül milyen elforgatási szög eredményez minimális hibát a két alapfelület közötti transzformációban? Ez a feladat iterációval oldható meg a legegyszerűbben, amelyet akár táblázatkezelő program segítségével, manuálisan is elvégezhetünk.

A skálatényezőt ezután a kezdőponton megadott, a helyi dátumra vonatkozó geoid-unduláció és a pontban érvényes ellipszoidi sugár hányadosával is becsülhetjük, vagy (amennyiben a vertikális pontosságra a feladat szempontjából érdektelen, vagy ha az említett unduláció-érték zérus), nullának is vehetjük.

Ezzel a módszerrel nemcsak megkerülhetjük a többdimenziós paraméterbecsléshez szükséges bonyolult matematikai eljárást, de a kapott paraméterek fizikai-geometriai jelentéssel is bírnak.

5. Térképek és vetületek

A térinformatika számára a térképek fontos adatforrást jelentenek. Sok esetben a térkép szkennelt formában, mint raszteres kép áll rendelkezésre, és az adatokat a kép információk hordozzák. Előfordul, hogy a térkép adatainak egy részét vektoros formában rögzíteni, digitalizálni szeretnénk. Az ilyen információk hasznosításához elengedhetetlen, hogy a térkép kiegészítő információit felhasználva geokódolni tudjuk annak tartalmát. Ebben a fejezetben felsoroljuk e kiegészítő információkat és megadjuk az értelmezésükhöz és kezelésükhöz szükséges ismereteket.

A térképek az alapfelület vetítéssel történő síkbafejtésének eredményei. Így minden térképnek kell hogy legyen alapfelülete, dátuma (4. fejezet), amelynek felszínét valamely vetület egyenleteinek felhasználásával síkba fejtjük. A térinformatikai szoftverek általában ismerik a fontosabb vetületek egyenleteit, így e fejezetben igyekszünk úgy áttekinteni a vetületeket, hogy azok egyenleteinek konkrét felhasználására az Olvasó, ha lehet, ne legyen rászorulva.

5.1 Vetületek és paraméterezésük

A Föld geoid-, illetve közelítőleg ellipszoid alakjának felszínét térképi ábrázolásokhoz síkba kell fejteni. Ez a művelet nem végezhető el torzításmentesen sem a gömb, sem az ellipszoid felszínéről. A síkba fejtés művelete a vetítés. A gömb, illetve az ellipszoid felszínének pontjait hengerpalástra, kúppalástra vagy síkfelületre lehet vetíteni, a henger- és a kúppalást pedig már síkba teregethető.

A vetületeket vetületi egyenletek valósítják meg. Ezek az egyenletek írják le a kapott síkoordináták (vetületi koordináták) és a gömbi vagy ellipszoidi koordináták közötti kapcsolatot. A vetületi egyenletek általános alakja a következő:

E=f₁(Φ,Λ,p_1,…,p_n);

N=f₂(Φ,Λ p_1,…,p_n).

Ahol E és N a vizsgált pont vetületi síkkordinátái. Az elnevezéssel (E: Eastings; N: Northings; tehát keleti és északi irányú koordináták) feltételezzük, hogy a vetített koordinátarendszer tengelyei keleti és északi irányba növekvő értékeket jeleznek, tehát a rendszer északkeleti tájékozású. Ez a legtöbb esetben igaz, a lényeges eltérésekre még visszatérünk. A térkép méretaránya a pontos definíciója: az a (általában 1-nél jóval kisebb) szám, amellyel a kapott E és N koordinátákat meg kell szoroznunk ahhoz, hogy a kívánt területet a térkép papírján ábrázolni tudjuk. Az

Φ=g₁(E,N,p_1,…,p_n);

Λ=g₂(E,N,p_1,…,p_n).

egyenletek a vetület ún. inverz egyenletei. Az f₁ és f₂, illetve a g₁ és g₂ függvények a vetület típusától függenek, és sokszor igen bonyolult alakúak. A térinformatikai gyakorlatban általában nem szükséges, hogy a vetületek konkrét alakját ismerjük, vagy hogy azokkal számolni tudjunk: az általunk használt térinformatikai szoftver, vagy adott esetben a GPS-vevő szoftvere általában ismeri ezeket, és elegendő, ha mi ismerjük ezek kezelését.

A vetületi egyenletek a gyakorlatban egzaktaknak tekinthetők, ami azt jelenti, hogy a direkt és az inverz egyenletek egymás utáni alkalmazásakor az eredeti koordinátákat milliméternél pontosabban kapjuk vissza.

A p_1,…,p_n paraméterek a konkrét vetülettől függenek, és a paraméterek számát a vetület típusa szabja meg. Például a transzverzális szögtartó hengervetületnek öt paramétere van, de a ferdetengelyű szögtartó hengervetületnek hat. Ezeket a paramétereket (általában 5 vagy 6 számot) és a vetület típusát vagy a használt szoftvernek, vagy – ami sokkal megnyugtatóbb – nekünk magunknak, ismerni kell. Lássuk, milyen paraméterek tartoznak a vetületekhez.

Bármilyen vetületre igaz, hogy tartozik hozzá egy ún. vetületi kezdőpont, amelynek ellipszoidi szélessége és hosszúsága két vetületi paraméter. A kezdőpont a sík, a kúp vagy a henger (tehát a képfelület) és az alapfelület érintési pontja. Amennyiben a képfelület az alapfelülethez képest forgásszimmetrikusan helyezkedik el, akkor a kezdőpont hosszúsága önkényesen választott, de a szabványosított vetületek esetén előre rögzített érték. Amennyiben az érintés egy vonal mentén történik, ezt a vonalat vetületi középvonalnak nevezzük.

További paraméter az ún. skálatényező. A vetítés ugyanis nemcsak érintő, hanem metsző helyzetű képfelületre is történhet (ebben az esetben a kezdőponttól, illetve a középvonaltól nagyobb távolságig tart az „elfogadhatóan alacsony torzulás” zónája). A képfelületet (síkot, kúpot, hengert) a skálatényezővel kicsinyítjük (a kivétel Írország, ahol nagyítás van), redukáljuk. Az érintési, illetve metszési pontokban nem lép fel torzulás.

A vetületi kezdőpont tényleges vetületi koordinátái, tehát a keleti és északi irányú eltolás, a „hamis” keleti és északi koordináták (FE: False Eastings; FN: False Northings), általában méterben értelmezett paraméterek. Ezek lehetnek zérus értékek is: az ettől való eltérést azért vezetik be, hogy a térképezett területen mindenütt pozitív vetületi koordináták legyenek, és esetleg az északi vagy a keleti koordináták közül az egyik a teljes térképezett területen nagyobb legyen, mint a másik („bolondbiztos” vetületi definíció).

A redukált kúpvetületek esetén a skálatényező helyett megadható annak a két paralelkörnek a szélessége, ahol a képfelület és az alapfelület metszi egymást, ezeket standard paralelköröknek nevezzük.

A ferdetengelyű hengervetületek vetületi kezdőpontja lehet a középvonalnak az Egyenlítőtől legtávolabbi pontja (Laborde-vetület) vagy az Egyenlítővel való metszéspontja (Hotine-vetület). A vetület definiálásakor általános értelemben a középvonal bármely pontja lehet a vetületi kezdőpont. Meg kell emiatt adni a középvonalnak a kezdőponton vett áthaladási irányát, azimutját. A középvonal definiálható kép adott pontjával is.

A vetületeket leíró szabványok sokszor említenek ún. kettős vetítést. Ekkor a vetületi egyenletek két lépésben írhatók fel. Első lépésben az ellipszoidról gömbre vetítünk, majd a gömbről a képfelületre. Ennek az az oka, hogy a számítógép előtti időben a közvetlen vetítés elvégzése túl bonyolult számításokat igényelne. Ez általában nem jelent gondot, a térinformatikai szoftverek által használt formulák nagyon jó közelítései a kettős vetítésnek, az eltérés a milliméter töredéke. Ha a gömb és az ellipszoid metszéspontjának szélessége (az ún. normálparalelkör) nem esik egybe a vetületi kezdőponttal, akkor a későbbiekben említett közelítő egyenletek módszerét használhatjuk.

A világon használt vetülettípusok száma több tízre tehető, ezek közül azonban csak néhány az, amely a topográfiai térképezésben használatos a világ országaiban. A következő bekezdésekben a három legelterjedtebb változatot: a transzverzális Mercator-vetületet, a Lambert-féle szögtartó kúpvetületet és a sztereografikus síkvetületet tekintjük át. Előrebocsátjuk, hogy mindhárom tárgyalt vetülettípus szögtartó, azaz egy adott tereptárgytól két másik ponthoz húzott terepi egyenes szöge megegyezik a terepi egyeneseknek megfelelő térképi görbe vonalaknak a tereptárgynál vett érintői által bezárt szöggel.

A transzverzális Mercator-vetület esetén a hengerpalást forgástengelye az Egyenlítő síkjába esik. A vetületi kezdőpont az Egyenlítőn van. Érintő esetben az alapfelület és a képfelület egy meridiánív mentén érinti egymást, ez a vetület középvonala. Ha a skálatényező 1 (például a Varsói Szerződés által korábban használt Gauss-Krüger vetület esetén), akkor a henger érintő helyzetű, és a középmeridián mindkét oldalán kb. 180 kilométerre nyúlik az a sáv, amelyen belül a hossztorzulások 1/10000 alatt maradnak. 1-nél kisebb skálatényező esetén (például az UTM; Universal Transverse Mercator, vetület esetén, ahol 0,9996) a hengerpalást metsző helyzetű, és az alacsony hossztorzulású sáv szélesebb. A kezdőpont vetületi koordinátái közül az északit rendszerint (de nem mindig!) nullának választják, a keletit pedig úgy definiálják, hogy az értelmezett tartományon sehol ne legyen negatív (pl. 500000 méter).

A Lambert-féle szögtartó kúpvetület esetén a kúppalást forgástengelye az alapfelületnek használt ellipszoid kistengelyével esik egybe. A vetületi középvonal a kúp és az ellipszoid metszésvonalát jelentő paralelkör (az ún. normálparalel) valamely kijelölt pontja. Ennek vetületi koordinátáit általában úgy választják meg, hogy a térképezett területen mindenütt pozitív koordináták adódjanak. Ezt a vetületet ritkán használják érintő változatban, általában egy 1-nél kisebb skálatényezővel redukálják. A vetület definiálható a kezdőponttal és a skálatényezővel, vagy a kezdőponttal és a két metsző paralellel, az ún. standard paralelkörökkel.

A sztereografikus síkvetület (Roussilhe-vetület) esetén az alapfelület valamely pontjához síkot illesztünk, és erre végezzük el a vetítést. A kezdőpont a sík és az ellipszoid metszéspontja. Ha a skálatényező 1 (érintő helyzet), akkor a kezdőpont körül kb. 127 kilométer sugarú körön belül marad 1/10000 alatt a hossztorzulás. 1-nél kisebb skálatényező (metsző sík) esetén ez a tartomány szélesebb lesz.

A felsorolt három (és az összes többi) vetület esetén tehát van olyan zóna, amelyben a hossztorzulás elfogadhatóan alacsony. A transzverzális Mercator-vetület esetén ez a zóna egy meridián mentén húzódó, észak-déli irányú sáv. A Lambert-féle szögtartó kúpvetület esetén a zóna egy paralel mentén húzódó, kelet-nyugat irányú sáv, míg a sztereografikus síkvetület esetén egy pont körüli, nagyjából kör alakú tartomány.

Amennyiben a térképezendő terület túlnyúlik ezen a sávon (pl. nagyobb országok, tartományok, vagy az egész Föld felszíne esetén) akkor több, eltérő kezdőponttal rendelkező vetületet definiálnak az egyes zónák számára. Például Franciaországban 4 darab Lambert-kúpvetület alkotja a 4, kelet-nyugati irányban elnyúló zónát. Németországban 5, Ausztriában 3 darab transzverzális Mercator-vetület alkotja az észak-déli irányú zónákat. Lengyelország 1965-ös zónarendszere 4 darab sztereografikus és egy transzverzális Mercator-vetületből áll. Ezeket a vetület-csoportokat vetületi rendszereknek nevezzük.

Kisebb országok esetén egy vetület is elegendő. Hollandia esetén elegendő egyetlen sztereografikus síkvetület definiálása. Romániában, bár az ország területe jócskán meghaladja a kis torzulás zónáját, szintén egyetlen sztereografikus vetületet definiáltak. Az országok, vagy a térképezendő tartományok alakja megszabhatja, hogy milyen vetületet érdemes választani annak érdekében, hogy egyetlen, de kellően alacsony torzulású zóna alkalmas legyen a térképezésre. Észak-déli irányban elnyúlt országok (pl. Chile, Portugália) a transzverzális Mercator-vetületet választották, míg kelet-nyugati irányban elnyúlt államok (mint Belgium vagy Észtország) számára a Lambert-vetület az alkalmas. Svájc és Magyarország ezért választott ferdetengelyű hengervetületet (bár a Lambert-vetület is alkalmas lenne egy zónának). A két világháború közötti Csehszlovákia (a mai Csehország és Szlovákia területe mellett Kárpátalja is ide tartozott) csak ferdetengelyű kúpvetület esetén volt egy zónába osztható.

A vetületi egyenletek felhasználásával készült térképen azok a vonalak, amelyek azokat a pontokat tartalmazzák, amelyek az északi vagy a keleti irányban azonos vetületi koordinátával bírnak (ún. vetületi koordináta-vonalak) egyenesek, és a két irány szerint egymásra merőleges egyenes-sereget alkotnak. A fokhálózati vonalak képe általában valamilyen görbe vonal. Csak bizonyos kitüntetett paralelkörök vagy meridiánok képe egyenes. A hálózati észak (a vetületi koordináta-vonalak északra mutató vége) és a földrajzi észak (a meridiánok képe) közötti szög az ún. meridián-konvergencia, amely általában helyről helyre változik (egyes vetületeknél, pl. a normál elhelyezésű Mercator-vetület esetében, mindenütt nulla). Mindig tartsuk észben, hogy még az olyan kisméretarányú térképek esetében is, amelyeken a vetületi koordináták nem, csak a fokhálózat van feltüntetve, a vetületi koordinátavonalak alkotják a láthatatlan „négyzethálót”.

5.2 Átszámítások különböző vetületi koordináták között

A vetületi koordináták közötti átszámítás elnevezés nemcsak a két vetület paramétereinek – illetve legalábbis a szoftverben, a felhasználó számára láthatatlanul – a vetületi direkt és inverz egyenletek ismeretét igényli, hanem a két vetület alapfelületeinek, a dátumoknak az egymáshoz képest értelmezett helyzetét is ismernünk kell. Ebből a szempontból az a legkönnyebb eset, ha a két vetület ugyanazon a geodéziai dátumon van értelmezve. A legtöbbször azonban nem ez a helyzet.

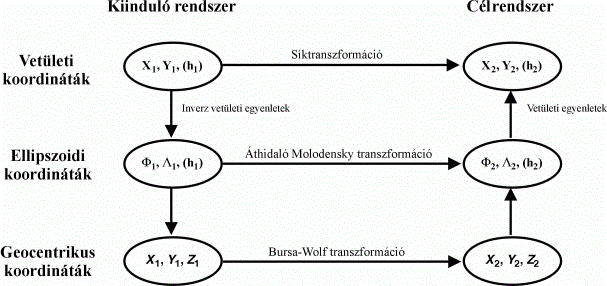
1. ábra. Vetületi koordináták közti átszámítások lehetséges útjai.

Az átszámítás három lehetséges módját az 1. ábra mutatja be. Természetesen, ha az alapfelület azonos, akkor a dátumtranszformációkra nincs szükség. Ha azonban a kiinduló és a céldátum különböző, akkor az ábrán feltüntetett utak valamelyikét kell válasszuk.

A közvetlen átszámításhoz azonos pontok különböző vetületi rendszerben értelmezett koordinátái alapján illesztett magasabbrendű polinomok együtthatóinak becslésén alapul. Itt ezzel az eljárással nem foglalkozunk, mert – bár pontossága a legjobb az összes lehetséges megoldás közül – mint már említettük, a térinformatikai szoftverek túlnyomó többsége nem támogatja ezt az eljárást.

A második lehetőség az, hogy a kiinduló vetület inverz egyenleteit felhasználva kiszámítjuk a kiinduló dátumon értelmezett ellipszoidi koordinátákat. Ezeket az áthidaló Molodensky-formulák segítségével átszámítjuk a céldátumon értelmezett ellipszoidi koordinátákra, majd a cél vetület egyenleteit használjuk arra, hogy ezekből vetületi koordinátákat kapjunk. Az átszámítás hibáját a dátumtranszformáció, tehát az egyes alapfelületeket megvalósító háromszögelési hálózatok belső torzulása közötti különbség okozza. Ezt az eljárást használja a legtöbb GPS-vevő beépített vetületszámító rendszere is, azzal a megkötéssel, hogy a bemeneti adat itt nem vetületi, hanem WGS84 ellipszoidi koordinátákból áll, így ebben az esetben az első lépés, az inverz vetületi egyenletek alkalmazása elmarad. Ezt az algoritmust alkalmazzák azok a térinformatikai szoftverek is, amelyek csak az egyszerűbb Molodensky-féle paraméterezést támogatják, de a bonyolultabb Bursa-Wolf-félét nem.

Amennyiben a Bursa-Wolf transzformáció paraméterei is a rendelkezésünkre állnak, és a szoftver ismeri ezt az eljárást, úgy a kiinduló dátumon értelmezett geocentrikus koordinátákat is ki kell számítanunk, majd ezeket a Bursa-Wolf transzformációt elvégezve alakítjuk a céldátumon értelmezett geocentrikus koordinátákká. A célrendszerben érvényes ellipszoidi koordinátákat ezekből a Borkovski- vagy a Bowring-féle formulákkal kaphatjuk meg. Az átszámítás hibája itt is a dátumtranszformáció hibájából származik. Az igen egyszerű, zárt Bowring-formula alkalmazása további, 1 centiméter körüli hibát okoz.

A gyakorlatban a legritkább esetben szorulunk arra, hogy ezeket az átszámításokat mi magunk végezzük el. A szoftverek beépített vetületkonverziós moduljai elvégzik helyettünk ezt a munkát, ugyanakkor tisztában kell lennünk azzal a használatukkor, hogy mi is történik „a doboz belsejében”.

5.3 Helyettesítő vetületek

A térinformatikai gyakorlatban előfordul, hogy az általunk használt szoftver nem ismeri a használni kívánt vetület típusát, és az sem ritka, hogy olyan adatot, térképet kell geokódolnunk, amelynek vetülete nem ismert. Ebben a pontban az ilyenkor követendő eljárást tekintjük át.

A szoftverekbe a kevésbé elterjedt, illetve kis piaci szegmenst jelentő országok vetületeit nem minden esetben építik be. A magyarországi EOV (Egységes Országos Vetület) speciális kettős vetítést tartalmazó rendszerének, vagy a korábbi Csehszlovákia által használt Krovák-féle ferdetengelyű kúpvetületnek a vetületi egyenletei sokszor nincsenek beprogramozva. Az egyszerű felhasználó nem tudja a fejlesztői csomagok felhasználásával maga programozni és a szoftverhez illeszteni ezeket. Azt viszont megteheti, hogy kiválaszt egy másik, a szoftver által használt vetülettípust, és annak paramétereit úgy választja meg, hogy az így definiált helyettesítő vetület és a valódi rendszer között a vizsgált területen a legkisebb legyen az eltérés. Az alábbiakban az említett két vetületi rendszer közelítésére mutatunk be esettanulmányokat.

A) Az EOV (Egységes Országos Vetület) helyettesítése Laborde- vagy Hotine-típusú ferdetengelyű szögtartó hengervetülettel

Az EOV szabványa szerint kettős vetítést tartalmaz: első lépésben az IUGG67 (GRS67) ellipszoidról az új magyarországi Gauss-gömbre, majd második lépésben a ferde elhelyezésű hengerpalástra vetítünk. Az ellipszoidról a gömbre vetítés érintő paralelköre (normálparalel) nem esik egybe a gömbről a hengerre történő vetítés vetületi kezdőpontjával. A térinformatikai szoftverekben a Laborde- és a Hotine-vetületek (van, ahol utóbbit RSO; Rectified Skew Ortomorphic; néven használják) gyakorlatilag az olyan kettős vetítésnek felelnek meg, ahol a normálparalel és a vetületi kezdőpont szélessége azonos. Az EOV speciális esete nincs beépítve e szoftverekbe, így az nem is paraméterezhető a szabványnak megfelelően.

Ha tehát az EOV-t be akarjuk építeni e programcsomagokba, akkor közelítő vetületet kell találnunk. A vizsgálatok azt mutatják, hogy a kettős vetítéssel származtatott vetület több nagyságrenddel érzékenyebb a kezdőpont megváltoztatására, mint a Gauss-gömb helyzetének módosítására. Emiatt a gömb és az ellipszoid érintési pontját megváltoztatjuk úgy, hogy az egybeessen a vetületi kezdőponttal. Az így definiált helyettesítő vetület az ország területén mindenütt 0,2 milliméter alatti hibával közelíti az EOV-koordinátákat. Ez nemcsak a térinformatika, hanem a szélső pontosságú geodéziai alkalmazások igényeit is kielégíti.

A Laborde-vetület paraméterezése az EOV-szabvány szerint egyszerűen megtehető: a vetületi kezdőpont ellipszoidi és vetületi koordinátái és a skálatényező mellett a középvonalnak a kezdőponton áthaladásakor fellépő 90 fokos azimutot kell megadni. A Hotine-vetület paraméterezése csak annyiban tér el ettől, hogy a kezdőpont keleti irány vetületi koordinátájából (False Eastings) ki kell vonni a kezdőpontnak és az Egyenlítőnek a középvonal mentén mért távolságát.

B) Az EOV helyettesítése Lambert-féle szögtartó hengervetülettel

A Laborde- és a Hotine-féle vetületek azonban nem különösebben elterjedtek, ezért több térinformatikai szoftverbe nem, vagy helytelenül építették be az egyenleteiket. A Lambert-féle szögtartó kúpvetület azonban eléggé elterjedt, ezért érdemes ennek paraméterezésével is közelítő vetületet keresni. Busics György vetette fel azt a gondolatot, hogy mivel a Lambert-kúpvetület középvonala normálparalelkörön fekszik, míg a ferdetengelyű hengervetület esetén a kezdőpontban ahhoz simul és az ország területén attól csak néhány méterre tér el, ez a helyettesítés használható. A gyakorlatban az EOV ismert paramétereit a normálparalelkörrel és skálatényezővel definiált Lambert-féle szögtartó kúpvetület paramétereiként is meg lehet adni. A közelítés maximális hibája az ország területén 2 méter alatt marad, tehát a térinformatikai pontosságigény teljesül.

C) Az EOV helyettesítése kis területen transzverzális Mercator vetülettel

Egyes GPS-vevők (pl. a Garmin-típusok) kizárólag a transzverzális Mercator-vetület paraméterezését teszik lehetővé a felhasználó számára, hogy a műszer által nem ismert, saját vetületet (User Grid) definiáljon. Takács Bence bemutatta, hogy - bár az eredeti és a közelítő vetület középvonala gyakorlatilag merőleges - egy 15-20 kilométer sugarú tartományban a speciálisan ahhoz a helyhez definiált paraméterkészlettel a térinformatikai pontosság elérhető. Az eljárás ebben az esetben a következő:

- megmérjük a GPS-szel a tartomány egy olyan központi pontjának a hosszúságát, amelynek ismerjük az EOV-koordinátáit (E_EOV; N_EOV);

- definiálunk egy transzverzális Mercator-vetületet, amelynek kezdőpontja az Egyenlítő és az előző pontban megmért hosszúsági kör metszéspontja, skálatényezője az EOV esetén ismert 0,99993;

- leolvassuk a mért pont koordinátáit ebben a vetületben (E_TM; N_TM);

- az imént definiált transzverzális Mercator-vetület kezdőpontjának vetületi koordinátáiként (FE: False Eastings; FN: False Northings) a

FE=E_EOV-E_TM;

FN=N_EOV-N_TM értékeket állítjuk be.

D) A budapesti sztereografikus vetület helyettesítése Roussilhe-féle vetülettel

A budapesti sztereografikus vetület esetén a közelítés problémája az A) pontban említett kettős vetítésből adódik: a normálparalel és a kezdőpont szélessége itt is eltérő, és az eltérés lényegesen nagyobb az EOV esetén definiáltnál. Az eljárás itt is ugyanaz: a paraméterezésnél figyelmen kívül hagyjuk az ellipszoidról a gömbre vetítés normálparaleljét, és csak a vetületi kezdőpont koordinátáit adjuk meg. A nagyobb szélességkülönbség miatt a hiba is nagyobb, de az ország területén sehol nem haladja meg a 2 centimétert.

E) A cseh-szlovák Křovák-vetület helyettesítése Lambert-féle szögtartó hengervetülettel

A Křovák-vetület ferdetengelyű szögtartó hengervetület, amelyet kizárólag a volt Csehszlovákiában és utódállamaiban használtak ill. használnak. A térinformatikai rendszerek túlnyomó része nem ismeri e a típus egyenleteit (és ha mégis, akkor éppen azért ismeri, mert ezt a vetületet beépítették). A vetületi középvonal Kárpátalja délkeleti sarkán kelet-nyugati irányú, ettől nyugat felé távolodva egyre inkább északi felé kanyarodik. Ilyen középvonalat más vetülettel nem lehet definiálni, ezért a közelítés csak érdemi hibával lehetséges.

A Lambert-féle szögtartó kúpvetület paraméterezésével közelítő vetületeket definiálhatunk külön-külön Szlovákia és Csehország területére (más-más paraméterkészlettel). Mivel Szlovákia területén a középvonal kevésbé tér el a Lambert-vetület esetén elvárt kelet-nyugati iránytól, a hiba itt kisebb lesz: átlagosan 6 méter, maximálisan pedig 12 méter, ami az 1:25000 méretarányú térképek vagy a Landsat ETM űrfelvételek (15 méteres pixelméret) esetén még elfogadható, pontosabb alkalmazásokban nem.

A csehországi közelítés átlagos hibája 40 méter, maximum 82 méter. 1:100000 méretarányú térképek, az SRTM domborzati modell (90 méteres pixelméret) vagy MODIS-űrfelvételek (250 méteres képpontok) a közelítés elfogadható.

Végezetül: amennyiben a geokódolandó térkép vetületéről nincs semmilyen metaadatunk vagy irodalmi információnk, akkor a fokhálózatához jól illeszkedő vetülettípust kell választanunk, és azt paramétereznünk.

5.4 A térképek szelvényezése és a szelvényezés által hordozott georeferencia

A nagyobb területet, pl. egy országot vagy az egész Föld felszínét ábrázoló, általában nagy vagy közepes méretarányú térképművek külön lapokból, szelvényekből állnak, amelyek a teljes célterületnek csak egy kisebb részét ábrázolják. Ekkor az egyes szelvények számozása is segít bennünket abban, hogy az egyes szelvények egymáshoz képest vett helyzetét megállapítsuk anélkül, hogy a vetületi koordináta-vonalakat vagy földrajzi fokhálózatot kellene figyelnünk. Olyan térképsorozatok is vannak, amelyek semmilyen koordinátát nem tartalmaznak, azonban a szelvények széleinek, és még inkább azok sarokpontjainak a szelvényszámozás ismeretében kiszámíthatjuk a koordinátáit.

A térképszelvények határait vagy vetületi koordináta-vonalak, vagy fokhálózati vonalak jelentik. Előbbi esetben a térképszelvény térképi része téglalap vagy négyzet alakú, a második esetben pedig az alak foktrapéz. A szelvényszámozás egyértelműen megszabja a határoló vonalakat és a sarkok koordinátáit a vetületi, illetve a második esetben az ellipszoidi koordináták szerint.

Magyarországon az EOV-térképek szelvényhatárát az EOV-hálózat vonalai adják (földrajzi fokhálózat nincs is ezeken feltüntetve). A Gauss-Krüger, illetve a régebbi sztereografikus vetületben készült szelvények határolóvonalai paralelkörök és meridiánívek. Ha nem topográfiai térképünk, hanem abból származtatott, vagy azt munkatérképnek felhasználó szkennelt adatbázisunk van, amelynek szelvényezése és szelvényszámozása valamelyik topográfiai térképműével megegyező, akkor a sarokponti koordinátákat akkor is ki tudjuk számítani, ha a térképen egyébként semmilyen koordináta nincs megadva.

Ugyanez a helyzet a Habsburg birodalom II. katonai felmérésének 1:28800 méretarányú felmérési szelvényeivel is. A térképeken nem találunk sem vetületi sem földrajzi koordináta-hálózatot, azonban a térképmű feltételezett vetületi rendszerében a szelvényszám egyértelműen meghatározza a sarokpontok koordinátáit a vetületi kezdőponthoz képest, így a szelvények első közelítésben terepi illesztőpontok nélkül is geokódolhatóak.

6. Térképek georeferálása

A térképek és térképi adatbázisok georeferálása azt jelenti, hogy a szkennelt raszteres képformátumú állomány képpontjait georeferenciával látjuk el. Kezdeti állapotban a szkennelt raszteres kép képpontjainak csak a kép síkkoordináta-rendszerében érvényes pixel-koordinátái vannak. Ebben a koordinátarendszerben (amely az egyes térinformatikai rendszerekben eltérő lehet) például a kép bal felső sarka kapja a (0,0) koordinátákat, és minden képpont 1-1 növekményt jelent a koordinátákban.

A georeferálás során illesztőpontokat (GCP; Ground Control Point) választunk, amelyeknek megadjuk mind a pixelkoordinátáit (a kép előbb említett koordinátarendszerében), mind pedig a térképi koordinátáit (a térkép vetületének koordinátarendszerében).

6.1 A georeferálás és a rektifikáció

Az illesztőpontok megadása során többféle eljárást választhatunk. Mindezekben közös, hogy elsőként meg kell határoznunk azt, hogy a képkoordinátákhoz milyen vetületben és milyen dátumon értelmezett koordinátákat rendelünk hozzá az illesztőpotokban. Már most meg kell jegyezzük, hogy lehetőség szerint azt a vetületet és dátumot válasszuk, amelyben a térkép készült, és ne azt, amelyben a végeredményt kell kapjuk. Azt is el kell döntsük, hogy az alkalmazott számítógépes program milyen eljárással illessze a vetületi koordinátarendszert az illesztőpontokra. A felkínált eljárások leggyakrabban a polinomiális illesztést használjuk, ennek válfajai:

· lineáris;

· kvadratikus;

· köbös.

A lineáris illesztés esetén illesztőpontjainkra egy egyenközű, de elforgatott négyzethálót illeszt a program. A kvadratikus és a köbös változat másod- illetve harmadrendű polinomillesztést használ. Ezekben az esetekben a konkrét illesztőpontokhoz történő maximális illeszkedés könnyebben elérhető, ugyanakkor az illesztőpontok között fellépő hibák is nagyobbak, továbbá az eljárás lényegesen több illesztőpont definiálását követeli meg. Ha csak lehet, a lineáris eljárást válasszuk.

A polinomiális illesztési módszer mellett a háromszögeléses illesztés is általában választható lehetőség. Ekkor az illesztőpontok helye fix, nulla hibával, az eljárás a képet az illesztőpontok között háromszögekre osztja, és minden egyes háromszög tartalmát külön-külön függvények segítségével illeszti.

Az illesztőpontok definiálására leginkább elterjedt, ugyanakkor a legnagyobb hibalehetőséget magában rejtő módszer az, ha a szkennelt térképen egyes tereptárgyakat felismerünk, és más adatbázisokból megszerezzük és megadjuk azok koordinátáit. Miért hordoz magában e módszer nagy hibalehetőséget? Azért, mert a térképeken, különösen a régebbieken az egyes tereptárgyak helye sokkal kevésbé pontosan meghatározott, mind a térkép „vázát” alkotó geodéziai alappontoké, és a térképi generalizáció következtében a tárgyak helyét sokszor csak 1-2 milliméteres térképi hibával határozhatjuk meg. Ezen túlmenően a módszer szinte csábít arra, hogy figyelmen kívül hagyjuk a térkép vetületét, amely, különösen kis és közepes méretarányú állományok esetén érdemi hibaforrás.

Ha a térképen adottak a vetületi koordináta-vonalak, és tudjuk az ezekhez tartozó koordináta-értékeket is, akkor a vonalak metszéspontjai (adott estben az őrkeresztek) szinte kínálják magukat illesztőpontoknak.

Ha ilyenek nincsenek, de a térképen megtaláljuk a földrajzi fokhálózat vonalait, akkor azok metszéspontjai (kerek szélességi és hosszúsági koordinátájú pontok) szintén alkalmasak illesztőpontnak. Amit nagyon meg kell jegyezzünk: ezekből az ellipszoidi koordinátákból ki kell számítanunk a vetületi koordinátákat (amennyiben erre a térinformatikai szoftverünk nem képes, akkor ez szinte az egyetlen olyan alkalmazás, ahol képeseknek kell lennünk a vetületi egyenletekkel ezek kiszámítására), és azokat megadni az illesztőpontokban. A földrajzi koordinátákat ilyen célra csak nagy torzulási hibát elkövetve használhatjuk!

Ha semmilyen koordinátát nem tartalmaz a térkép, de a szelvényezés adataiból kiszámíthatóak a sarokpontok koordinátái (az EOV bevezetését megelőzően készült magyarországi geológiai vagy erdészeti térképek sok esetben ilyenek), akkor a négy sarok vetületi koordinátáit kiszámítva azokat is használhatjuk illesztőpontnak.

Ha még ez sem áll fenn, akkor nincs más választásunk, mint az elsőként említett, tereptárgyak koordinátáin alapuló eljárás követése.

Ahogy az illesztőpontokat kijelöljük, a szoftver megadja, hogy az egyes pontoknak az összes (bekapcsolt) illesztőpontra illesztett koordináta-rendszerben mekkora a hibája. Kiugróan magas pontbeli hiba esetén vizsgáljuk meg, nem írtunk-e be hibás koordinátát, vagy nem azonosítottuk-e félre valamely pontot. Arra is figyeljünk, hogy az illesztőpontok ne essenek közel egy vonalba, hanem valós síkbeli szóródást mutassanak.

Ha legalább 5-6 (bilineáris és affin esetben legalább 8-10), a teljes állományon jól elosztott pontot definiáltunk, és azok hibája megfelelően alacsony (pl. max. 2 pixel), akkor a következő lépés a rektifikáció. Ennek során a számítógép elhelyezi az illesztett koordináta-rendszert a raszteres állományra, és az általunk megadott rácsmérettel az eredeti állományt átmintavételezi. Ennek eredménye egy olyan állomány lesz, amelynek képsorai és –oszlopai a választott koordinátarendszer tengelyeivel párhuzamosak, a pixelek mérete pedig megfelel az általunk megadott rácsméretnek.

Szintén a felhasználó adhatja meg az átmintavételezés algoritmusát. Ennek leggyakoribb lehetséges módszerei:

• legközelebbi szomszéd (NN: Nearest Neighbour);

• bilineáris;

• konvolúciós.

Az NN-módszer azt jelenti, hogy az átmintavett kép minden pixele azt az értéket veszi fel, amely a középpontjához legközelebb eső, eredeti pixel értéke (ÁBRA). Ez a leggyorsabb eljárás a három közül. Az eljárás garantálja, hogy az átmintavett kép pixelei csak olyan értékeket vehetnek fel, amelyek az eredeti képen is megvannak. Így amennyiben az egyes pixelértékek kategóriákat, például egy osztályozott űrfelvételen felszíntípusokat jelentenek, mindenképpen ezt a módszert érdemes választani.

A bilineáris algoritmus ebben az esetben azt jelenti, hogy az eredeti képek pixelértékei között lineáris interpolációval adja meg az értékeket, és ezeket rendeli hozzá az átmintavett kép pixeleihez (ÁBRA). Ez a módszer különösen akkor hasznos, ha az eredeti képhez képest lényegesen finomabb felbontást akarunk használni.

A konvolúciós eljárás lényege az, hogy az átmintavett kép pixelrács-hálóját az eredeti képre helyezi, és az eredménypixelek értékét az eredeti pixelértékeknek a területtel súlyozoztt átlagaként határozza meg (ÁBRA). Amennyiben az eredeti kép pixelértékei valamilyen folyamatosan változó, mért értékeket jelentenek (pl. űrfelvételek csatornáin mért radianciát), akkor az eljárás az NN-nél finomabb átmintavételezést jelent az erdeti pixelek méretével nagyjából megegyező, vagy azt meghaladó rácsháló esetében.

A szoftver – általában a saját formátumában – tárolja is az átmintavett állománynak a definiált koordinátarendszerben érvényes helyzetét (ÁBRA, ER Mapper ERS). Léteznek több szoftver által ismert, a koordinátarendszerben érvényes helyzetet leíró kvázi szabványok. Ilyen pl. az ún. „World File”, amelyet egyaránt alkalmaznak TIFF, JPEG típusú képfile-ok vagy akár MrSID-formátumú tömörített állományok leírására is, és amelynek rendkívül egyszerű szerkezete a következő:

A file 6 adatot tartalmaz, amelyek a következők:

- 1 pixel jobbra lépéskor az Eastings növekménye;

- 1 pixel lefelé lépéskor az Eastings növekménye;

- 1 pixel jobbra lépéskor a Northings növekménye;

- 1 pixel lefelé lépéskor a Northings növekménye;

- A bal felső sarok Eastings koordinátája;

- A bal felső sarok Northings koordinátája.

A file kiterjesztésére vonatkozóan nincs kötött szabály (bár a TWF, JWF és SWF az elterjedt változatok a TIFF, JPG és MrSID képekhez tartozó World File-ok esetén, de pl. a JPG mellett a JGW változat is előfordul). A World File nem tartalmazza a vetület/dátum kódját, azt magunknak kell kezelnünk. Figyeljük meg, hogy az első négy adattal a koordinátasík elforgatása is kezelhető.

A rektifikált (átmintavett) állományról a szoftver rögzíti, vagy számára meg kell adjuk, hogy annak koordinátarendszere milyen vetületben/dátumban értelmezett. Ennek alapján a szoftverek képesek azt egy másik vetületbe/dátumra átszámítani, természetesen csak akkor, ha mind a kiinduló, mind pedig a cél vetület/dátum paraméterei (4. és 5. fejezet) meg vannak adva.

Példa: a fentiek ismeretében tehát, ha egy szkennelt Gauss-Krüger 34. zónabeli vetületű (Pulkovo dátumú) térképre EOV vetületben (HD72 dátumon) van szükségünk, akkor a következő lépéseket kell megtegyük:

a) definiáljuk, hogy az illesztőpontok a Gauss-Krüger 34. zóna vetületében, Pulkovo dátumon lesznek megadva, pl. lineáris illesztési móddal;

b) megadjuk az illesztőpontok képi és Gauss-Krüger-koordinátáit;

c) rektifikáljuk (átmintavételezzük) a képet a Gauss-Krüger koordinátarendszerbe;

d) áttranszformáljuk az átmintavett képet az EOV-rendszerbe.

Ismét felhívjuk a figyelmet arra, hogy nem helyes, és illesztési hibát okoz az, ha a Gauss-Krüger-vetületű térképen eleve EOV-illesztőpontokat jelölünk ki. Ennek az az oka, hogy a Gauss-Krüger-térképen az EOV-koordinátavonalak képe nem egyenes, hanem valamilyen görbe vonal. Kis, néhány kilométer kiterjedésű területeken ez nem okoz észrevehető hibán, azonban több pl. száz kilométer távolságon a görbe vonalakban jelentkező húrmagasság több tíz méter is lehet (ÁBRA), amely semmilyen módon nem korrigálható. A fent ismertetett a)-d) pontok alkalmazásával ezt a hibát elkerülhetjük.

6.2 A vetületi analízis és az önkényes vetületválasztás

Gyakran előforduló eset, hogy a georeferálandó térkép vagy más raszteres állomány valódi vetületét nem ismerjük. Koordinátarendszerbe illesztérsre azonban ebben az esetben is szükség van. Ehhez viszont meg kell tudnunk, vagy ha ez nem lehetséges, meg kell becsülnünk az állomány vetülettípusát és paramétereit, illetve szükség esetén a geodéziai dátumát is.

Mielőtt a térkép vagy az adatrendszer vetületét/dátumát ismeretlennek deklaráljuk, próbáljuk irodalmi vagy térképészeti adatok alapján kinyomozni azt. Keressünk a vetületre utaló adatokat a térkép szöveges részében. Előfordul, hogy a vetülettípust megadják, de a paramétereket nem. Olyan esettel is találkozhatunk, hogy utalnak a nemzeti vetületre/dátumra, de nem ismertetik annak definícióját, ekkor irodalmi kutatás vagy internetes böngészés is segíthat. Topográfiai térképek a legritkább esetben készülnek „kitalálhatatlan” vetülettel (bár a hazai turistatérképek azért szép feladatot jelentenek az elemző számára). Az adott ország nemzeti vetületi rendszere és a kapcsolódó dátum akkor is jó kiindulópont, ha ez a térképen nincs feltüntetve. Ha egy országban több vetületi rendszert is használtak az adott időszakban, akkor mindegyiket érdemes megvizsgálni. A szelvényezés számadatai is segíthetnek a pontos vetület kiválasztásában.

Hazánkban például egy-egy térkép vagy adatrendszer lehetséges vetületei általában: EOV, katonai Gauss-Krüger vagy budapesti sztereografikus vetület. Az EOV-vetületet 1975-ben vezették be, ezt megelőzően tehát nem készült ilyen térkép. A Gauss-Krüger vetületben készült topográfiai alapot az 1960-as évektől kezdve polgári célokra is felhasználták, maga a koordináta-rendszer azonban titkos volt, így ezeken a térképeken vagy nincs koordináta-megírás (a szelvények sarokponti koordinátái viszont számíthatók), vagy a sztereografikus koordináták vannak feltüntetve. Ha a szelvényszám „L/M-33/34”-gyel kezdődik (az osztásjel itt vagylagosságot jelent) akkor a térkép Gauss-Krüger vetületű. Az 1:75000 méretarányú sztereografikus térképek szelvényszáma négyjegyű, az 1:25000-eseké egy kötőjel utáni, 1-4 közötti számjeggyel egészül ki, és a földrajzi hosszúságok sok esetben ferrói kezdőmeridiánnal vannak jelölve. A hazai turistatérképek is legtöbbször a Gauss-Krüger topográfiai alap bázisán készültek, azonban a térképek úgy vannak elforgatva, hogy a négyzetháló (amely semmilyen vetületnek nem felel meg) északi iránya a mágneses észak felé mutasson.

Ha az ismeretlen vetületű térkép által ábrázolt terület kicsi, akkor gyakorlatilag mindegy, hogy milyen vetületet választunk. 10-20 kilométeres távolságon belül a fellépő húrmagasságok nem fogják meghaladni a térinformatikai pontosságot veszélyeztető 5 méteres mértéket. Ebben az esetben inkább a geodéziai dátum megválasztására ügyeljünk, ennek paraméterezéséhez azonban egyetlen illesztőpont is elegendő. A dátumellipszoid méretei szintén alig befolyásolják a pontosságot, az elhelyezést pedig úgy kell beállítanunk, hogy kezelje a fellépő vízszintes eltolásokat.

Ha a térképünk méretaránya kicsi, és így viszonylag nagy területet fog át, akkor abból a szempontból szerencsés a helyzetünk, hogy a térképi leolvasás fél milliméteres pontosságának, vagy a szkennelt pixelek terepi méretének megfelelő távolság több száz méter is lehet, tehát bármilyen vetületet kiválaszthatunk, amely az adott területen ilyen pontossággal megközelíti a térkép valódi vetületét. Több száz méteres pontossági határ mellett a geodéziai dátumválasztás gyakorlatilag mindegy. A vetületválasztáshoz a fokhálózat elemzésére van szükség.

Közepes szélességeken (pl. Európában) az áttekintő térképeken a paralelkörök képei nagyjából koncentrikus körök, a meridiánok pedig a pólus irányába mutató, közel egyenes vonalak, és az egyenlő hosszúságkülönbségű meridiánívek képe közötti szög is egyenlő. Ebben az esetben akkor is közelíthetjük a térkép vetületét Lambert-féle kúpvetülettel, ha a térkép maga nem abban készült.

Gyakori hiba, hogy csak földrajzi fokhálózatot tartalmazó térkép georeferálását sokszor a paralelkörök és meridiánok metszéspontjainak földrajzi koordinátái szerint végzik el. Ez helytelen és nagy hibára vezető eljárás. Helyesen ilyenkor a fokhálózati vonalak futását figyelembe véve meg kell becsülni a térkép vetületét és annak paramétereit. A fokhálózati vonalak metszéspontjain a földrajzi koordinátákból ki kell számítani az e vetület szerinti síkkoordinátákat, és a georeferáláskor azokat megadni az illesztőpontok koordinátáiként. A legtöbb térinformatikai rendszer lehetővé teszi azt, hogy a földrajzi koordináták beírása után azokat automatikusan vetületi koordinátákra transzformáljuk.