Estonia – Geographical Studies 9: 99-106
(2004)
Edited by KAARE, T. & PUNNING,
J-M.
ISSN 1406-6092
Gábor TIMÁR1,*, Raivo AUNAP2, Gábor MOLNÁR1
1Space Research Group, Dept. of Geophysics, Eötvös University of Budapest, Hungary
2Dept. of Geography, University of Tartu, Estonia
Introduction
In the 19th and 20th
century the history of Estonia was very unsettled and as a mirror of this, the
geodetic network has been changed a few times. Starting with C. Tenner’s and W.
Struve’s triangulation in 1811/1816-1819, Estonia has been covered by several
geodetic networks (Treikelder, 2000). During the independence between the two
World Wars, Estonia developed its own geodetic network, re-equalised in 1937.
Skipping here the short period of the first Soviet invasion and the German
occupation – and the geodetic works of the German Army Grid as well –, the
long-lasting Soviet occupation resulted a new geodetic system. This was the
Russian Pulkovo 1942, which was widely used not only in the former Soviet Union
but also in the countries of the later dissolved Warsaw Pact. After re-gaining
its independence, Estonia developed a new three-dimensional geocentred geodetic
system EUREF-EST92 and its realisation EUREF-EST97 derived by GPS measurements
(Randjärv, 2002, pp. 13-15).
In this paper the geodetic datum
parameters are presented between the world’s quasi-standard, the geocentred
WGS84 datum and some older datums, and the Eesti Vabariigi Triangulatsioon as
well. These data set enables to fit the old Estonian maps to the modern ones in
GIS packages without using selected ground control points but using instead the
indicated grid values and crosshairs only. Errors are described where possible.
The concept of
geodetic datums and datum transformations
As the Earth’s surface is not a
perfect ellipsoid but a complex mathematical shape called geoid, the
ellipsoid-based triangulation and geodetic systems have to approximate the
geoid with an ellipsoid, and this approximation is valid with low error only in
the surveyed area.
After choosing an ellipsoid (fixing
its semimajor axis and flattening), the coordinates of several basepoints are
determined by triangulation. In some points of this network (the so-called
’Laplace-points’) the astronomical coordinates are also measured directly.
Because of the shape difference between the geoid and the ellipsoid, the
astronomical and the triangulation coordinates do not match. These differences
are spread on the survey area by the equalisation process.
The result of the geodetic
equalisation is an ellipsoid with the pre-defined semimajor axis and flattening
with a relative displacement and orientation. Relative means here that
the geometric centre of the ellipsoid is not at the Earth’s mass centre and the
network North is not exactly the true North. If the same area is surveyed
repeatedly using different ellipsoids with different shape (as has been done in
Estonia, too), the geometric centres of the different ellipsoids are different,
as well as the orientation of the network Norths.
Using the GPS technique, we are able
to determine our position relative to the real mass centre of the Earth. The World Geodetic System 1984 (WGS84; DMA 1986)
is a true Earth centred ellipsoid via the orbit elements of the GPS satellites.
That’s why all local datums are parametrised with their transformation
parameters to the global WGS84 datum.
These transformations can define the
ellipsoid’s displacement only (simple ellipsoid shifts, 3-parameter or
Molodensky-Badekas [MB] models) or the displacement, the orientation
and the scale factor, too (shifts with rotation, 7-parameter or Bursa-Wolf
models). In the next two chapters, both transformation types are described. For
both, it is necessary to use the geocentric coordinates (Cartesian coordinates
with the zero in the center of the ellipsoid, X-axis pointing to the crossing
of the Equator and the null meridian, Y-axis pointing ro the crossing of the
Equator and the Eastern meridian of 90 degrees, Z-axis pointing to the North
Pole):
(1)
(2)
(3)
where 
the radius of
curvature in prime vertical; a and e are the semimajor axis and
the eccentricity of the ellipsoid; Φ, Λ and h are the
latitude, longitude and ellipsoidal height of the point; X, Y and
Z are its geocentric coordinates. For the reverse (geocentric to
geodetic) conversion, the exact solution of Borkowski (1989) and the simpler
but more approximative one of Bowring (1976) can be used. Both datum
transformation methods are interpreted on geocentric coordinates.
The Bursa-Wolf
(7-parameter) transformation model
For the transformation of the
geocentric coordinates of a given point on a certain datum to the ones on
another datum, Bursa (1962) and Wolf (1963) suggested a simplified form of the
three-dimensional Helmert-transformation. As it is a simplification, the
Bursa-Wolf method can be used in case of very small (several arc second order)
rotations, as follows:
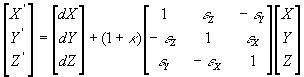(4)
where X’, Y’
és Z’ are the geocetric coordinates on the target datum, dX, dY
and dZ are the shifting, εX, εY
and εZ are the rotation parameters, κ
is the scale factor.
It has to be underlined that the
sign convention of the rotation parameters can be of two kinds: the one
represented in this equation is the coordinate frame rotation
convention, mostly used in the USA and Australia (and therefore, by the common
GIS packages, too). The other one, the position vector rotation
convention (used in Western Europe and also proposed by the ISO19111 draft) is
very similar but all rotation parameters have a reversed sign in the (4)
equation and in the parameter set. For converting a parameter set from one
rotation convention to the other one, the only thing to do is to change the
signs of the rotation parameters.
The
Molodensky-Badekas (3-parameter) transformation model
If we suppose that the source and
the target datums (ellipsoids) have parallel axes, Equation (4) will be simplified
to a simple three-dimensional shift (Badekas, 1969) as
(5)
and
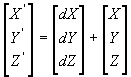(6)
Moreover, in this
case it is not necessary to deal with the geocetric coordinates. Using the
so-called abridged Molodensky-formulas (Molodenskiy et al., 1960; DMA,
1990), the transformation can be made as follows:
(7)
(8)
(9)
where 
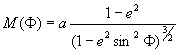the radius of
curvature in prime meridian; ΔΦ” and ΔΛ” are the latitude-
and longitude difference between the geodetic coordinates on the source and
target datums, Δh is the difference between the ellipsoidal
heights, a and f are the semi-major axis and the flattening of
the source datum, da and df are the differences between the
semi-major axes and flattenings of the source and target datums. N and e
are described after Equation (3). If ellipsoidal heights are not presented,
they can be computed using global or local geoid models, or Equation (9) can be
simply skipped.
The used datasets and methods
For the determination of the
parameters of the Estonian 1937 datum, coordinates of several geodetic stations
throughout Estonia were provided by the National Land Survey. After the
evaluation, 74 of them occurred identical both in the old (1937) and new (1992)
systems.
For each points, the L-EST97 coordinates were presented along with the old Estonian Lambert coordinates of the respective zone. The older coordinates are fit to a system with zero False Eastings and False Northings, instead of the known cartographic description (Jürgenson, 1997). Geodetic coordinates of the points on both datums were computed using the projection equation, based on the work of Snyder (1987).
No elevation data were presented at the basepoints. In horizontal investigations it is not necessary, so no altitude reference was used in the computation of the horizontally best fitting MB parameters. In computing the MB parameters using the fundamental point of a datum, the WGS84/GRS80 ellipsoid height was estimated using the EGM96 global geoid model (NIMA, 1997) while the ellipsoidal height based on the local datum was set to zero. In computing the Bursa-Wolf parameters, the elevation data of all points on the local datum were set to zero while the ellipsoid heights of the points were set to 17 m as a countrywide average of geoid undulation on the WGS84/GRS80 ellipsoid.
For the parameters of the
Triangulation of the coast of the Baltic Sea, the Triangulation of Finland and
St. Petersburg Territory (of Russia), the Baltic Sea Triangulation and the
Russian Pulkovo 1942 datum, data of the respective fundamental points given by
Treikelder (2000) were used.
Parameters of
some older systems (1838-1915)
In case of the older
system, simple MB type parameter sets can be computed using the known
coordinates of the respective basepoints on the old system and on a new one
(S-42 or WGS84) as well. If the coordinates of the orientation points are known
also on a modern datum, a seven-parameter solution can be reached – but in this
case these data were not available.
The fundamental point
of the Triangulation of the coast of the Baltic Sea (1829-1838) is the
Observatory of Tallinn and its old and also its WGS84 coordinates are described
by Treikelder (2000). The computed three-parameter datum transformation
description is given in Table 1, column 2, along with the parameters of the
Walbeck ellipsoid. Without information on the zero meridian of Tallinn
observatory, the longitude of the fundamental point has been set to
L=24°47’32.55”, its approximate GRS-80 value calculated by Treikelder (2000).
The fundamental point
of the Triangulation of Finland and St. Petersburg
Territory (1891-1903)
and the Baltic Sea Triangulation (1910-1915) is the
dome hall centre of the Pulkovo Observatory. The coordinates of the same point
on the S-42 datum is known as well (Treikelder, 2000). Transformation
parameters between these datums and S-42 and WGS84 are given in Table 1. Having
no more basepoint data, we did not compute the errors of these parameter sets.
In case of the older Baltic Sea datum, the Pulkovo zero meridian value was set
to L=30°19’42.09”, its S-42 value.
|
transfor- mation |
CBS--> GRS80 |
FSP1903 --> S-42 |
BST1915 --> S-42 |
S-42 --> GRS80 |
FSP1903 --> GRS80 |
BST1915 --> GRS80 |
|
dX (m) |
+822 |
+389 |
+361 |
+22 |
+411 |
+383 |
|
dY (m) |
+380 |
+228 |
+275 |
–128 |
+100 |
+147 |
|
dZ (m) |
+649 |
+664 |
+664 |
–87 |
+577 |
+577 |
|
ellipsoid |
Walbeck1819 |
Bessel1841 |
Bessel1841 |
Krasovski |
Bessel1841 |
Bessel1841 |
|
a (m) |
6376896 |
6377397.155 |
6377397.155 |
6378245 |
6377397.155 |
6377397.155 |
|
1/f |
302.78 |
299.1528 |
299.1528 |
298.3 |
299.1528 |
299.1528 |
Table 1. Molodensky-Badekas datum transformation
parameters between some historical Estonian and modern datums. The ellipsoid
and its semi-major axis and inverse flattening values of the first
datums are also indicated. Abbreviations: CBS1838 – Triangulation of
the coast of the Baltic Sea;
FSP1903 – Triangulation of Finland and St. Petersburg
Territory; BST1915 – Baltic Sea Triangulation.
Note that in case of CBS1838 and FSP1903 the Tallinn and Pulkovo zero meridians have been set to
the modern longitude of those points.
The Estonian
1937 system
A new geodetic basis was adjusted for the
Historical Lambert projection as a result of triangulation on the Bessel1841
ellipsoid, conducted by Ottomar Douglas. The Varesmäe first-order triangulation
point was selected as the fundamental point of the datum. Its coordinates:
Φ = 59° 18’ 34.465”
Λ = 26° 33’ 41.441”
|
EESTI37--> GRS80 |
1. 7-params (all points) |
2. 7-params (52 points) |
3. 3-params (DMA, 1986) |
4. 3-params (Varesmäe) |
5. 3-params (best fit) |
|
dX (m) |
+390.14 |
+385.21 |
+374 |
+372.87 |
+388.28 |
|
dY (m) |
+183.39 |
+183.97 |
+150 |
+149.23 |
+156.92 |
|
dZ (m) |
+592.36 |
+598.51 |
+588 |
+585.29 |
+613.91 |
|
κ (ppm) |
–3.4158 |
–3.9077 |
0 |
0 |
0 |
|
εX
(arc sec) |
–0.9298 |
–0.8471 |
0 |
0 |
0 |
|
εY
(arc sec) |
+0.3536 |
+0.1587 |
0 |
0 |
0 |
|
εZ
(arc sec) |
+0.3099 |
+0.4665 |
0 |
0 |
0 |
|
average error |
0.59 |
0.17 |
0.79 |
0.85 |
0.56 |
|
max. error |
2.32 |
0.69 |
3.53 |
1.78 |
2.10 |
Table 2. Datum transformation parameter sets between
the Eesti Vabariigi triangulatsioon (EESTI37) and the GRS80 (practically
identical to WGS84).
Evalutaing the results, at first
sight it can be surprising that any 3-parameter solution can be better than a
7-parameter one. However, these sets were computed applying different methods:
7-parameter type ones are optimized to the best three-dimensional fit and the
’best fit’ 3-parameter set was optimised for the best horizontal fit. The
errors indicated in Table 2 are horizontal ones.
Nevertheless in GIS applications it
is suggested that the transformation No. 4 in Table 2 be used. As its error is
low enough for GIS usage, it is valid also in the three-dimensional space. In
spite of its lower average horizontal error, the three-dimensioal validity is
definitely not true for the transformation No. 5; esimating the ellipsoidal
heights, this one results in an error of several-metres.
The Pulkovo 1942
(S-42) system
The Bursa-Wolf type transformation parameter set between S-42 and WGS84
valid for Estonia is provided by Aunap (2001). For the parametrising of the
older systems, a simple datum shift parameter set was computed. This set is
primarily valid only in Estonia but as Pulkovo is not too far from this region,
the set has been assumed to be valid also for that point. The 3-parameter set
is given in Table 1, Column 5. The errors of this set is not estimated as we
had no more basepoint data, just the coordinates of the fundamental point.
Using the datum
parameters in the GIS and GPS practice
The correct usage of the datum
parameters – along with the map projections – enables to georeference the
historical maps and to fit them to modern ones without ground control points.
For the practical use, the most important capability is to fit the old maps
from the 1930s to the modern ones automatically, using only the map grid lines.
This could be a useful tool for the geographic reaseach of the change of
natural and built environment.
Most GPS receivers enable to set
‘user datums’ based on the 3-parameter datum transformation parameters. For the
EESTI37 and S-42 systems it may have practical importance to set them into GPS
receivers for the fieldwork.
References
Aunap, R. 2001. Bursa-Wolf transformatsiooniparameetrid Eestis
kasutatavate geodeetiliste daatumite jaoks. Manuscript, URL:
http://www.ut.ee/~raivo/estonia.htm
Badekas, J. 1969. Investigations related to the
establishment of a world geodetic system. Report 124, Department of
Geodetic Science, Ohio State University, Columbus.
Borkowski, K. M. 1989. Accurate algorithms to
transform geocentric to geodetic coordinates. Bulletin Géodésique 63:50-56.
Bowring, B. 1976. Transformation from spatial
to geographical coordinates. Survey Review XXIII:323-327.
Bursa, M. 1962. The theory for the
determination of the non-parallelism of the minor axis of the reference
ellipsoid and the inertial polar axis of the Earth, and the planes of the
initial astronomic and geodetic meridians from the observation of artificial
Earth satellites. Studia Geophysica et Geodetica 6:209-214.
DMA, Defense Mapping Agency. 1986. Department
of Defense World Geodetic System 1984 – Its Definition and Relationships With
Local Geodetic Systems. Technical Report 8350.2. St. Louis, Missouri, USA.
DMA, Defense Mapping Agency. 1990. Datums,
Ellipsoids, Grids and Grid Reference Systems. DMA Technical Manual 8358.1.
Fairfax, Virginia, USA
Jürgenson, H. 1997. Eestis kasutatud
kaardiprojektsioone ja koordinaatsüsteeme. Geodeet 14(38): 9-12.
Molodenskiy M. S., Eremeev, V. F., Yurkina, M.
I. 1960. Metody izucheniya vnesnego gravitatsionnogo polya i figuri Zemli. Trudy
CNIIGAiK [Moscow], vyp. 131.
NIMA, National Imagery and Mapping Agency,
National Aeronautics and Space Administration GSFC. 1997. WGS84 EGM96 (complete
to degree and order 360) 1st Edition. NIMA-NASA GSFC, St. Louis,
Missouri, USA
Randjärv, J. 2002. Geodeesia IV. Kohalik geodeetiline
põhivõrk. Tartu, 243 p.
Snyder, J. P. 1987. Map Projections – A Working
Manual. USGS Prof. Paper 1395
Treikelder, I. 2000.
Ülevaade Eestis kasutatud geodeetilistest daatumitest ja ristkoordinaatide
süstemidest. Geodeet 21(45): 28-30.
Wolf, H. 1963. Geometric connection and
re-orientation of three-dimensional triangulation nets. Bulletin Géodésique
vol. 68:165-169.