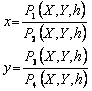
Űr- és légifelvétel geokódolása, ortorektifikáció

Nagy és szupernagy felbontású felvételek ortorektikfikációja kameramodell segítségével

E módszerhez nyers, előfeldolgozatlan felvétel, a kameramodell ismerete, digitális domborzati modell és néhány illesztőpont szükséges. A nyers felvétel általában elérhető (pl. SPOT). A kameramodell alkalmazása az előző fejezetekben ismertetett direkt- és inverzfeladat megoldás alapján érthető meg.  A műhold pályáját nem elég a pályaparaméterek segítségével meghatározni, mert a meghatározás hibája (100-500 méter) meghaladja a pixelméret többszörösét. Amíg a kisfelbontású felvételeknél a műhold tájolásának pontatlansága az egész felvételnél állandónak tekinthető, nagy és szupernagy felbontás esetén figyelembe kell venni annak időbeli változását egy felvételen belül. A műhold tájolásának hibáit leíró szögeket (α: a pálya érintőjének a műhold előrenéző tengelyével bezárt szögét; β: a műhold függőleges irányba tájolt tengelyének a helyi függőlegestől való eltérésének a pályasíkban mért; γ: pedig a pályasíkra merőlegesen mért szögét) az idő lineáris függvényének tekintik. Ezért a műholdpályát és a műhold pozicióját a szükséges pontossággal illesztőpontok segítségével határozzák meg. Ennek során a műholdpályát úgy módosítják, hogy az illesztőpontokra a mért és a képi koordinátákhoz számított vetületi koordináták eltérése minimális legyen. Ezt a javított műholdpályát alkalmazzák a direkt és az inverz feladat megoldásakor, utóbbihoz a magasságot a domborzati modellből nyerik. Az eredménykép a valamennyi torzító hatástól mentes ortorektifikált kép, amelynél a hiba 1-1,5 pixel nagyságú.

Az Ikonos műholdképek megjelenését követő várakozásokat lehűtötte a Space Imaging cég döntése, hogy nem teszi közzé a felvételekhez tartozó kameramodellt. A döntést az indokolhatja, hogy így ellenőrizni tudja a nagyobb pontossági igényeket kielégitő „Ikonos Precision Plus” termékek előállítását. Az olcsó, alacsony feldolgozottságú képek felhasználásának és a nagy pontosság elérésének igénye arra ösztökélte a kutatókat, hogy megpróbálják maguk meghatározni a kemeramodell paramétereit. Az Ikonos műhold nyilvánosságra hozott pályaparamétereiből és magukból a felvételekből (a pixelméret változása alapján) sikerült visszaállítani a leképezési geometriát (Toutin és Cheng, 2000) és ortorektifikálni a felvételeket.

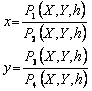
ahol P_i az X,Y és h koordinátákból alkotott első-, másod- vagy harmadfokú polinom. (Dowman és Tao, 2002). Az egyenletek alakjából látszik, hogy elsőfokú esetben alakjuk megegyezik a légifényképek kiértékeléséhez használt egyenletekkel (pl. Detrekői, 1991). A magasabb fokszám alkalmazásával próbálják figyelembe venni az űrfelvételek bonyolult – nem centrális – leképezési geometriáját. A módszert – az azt kifejlesztő kutatói csoport ajánlására (OGC, 1999) – több térinformatikai szoftverbe is beépítették (LH System SOCET Set, ERDAS, PCI, Rational Mapper). Az alkalmazás során az egyenletekben szereplő együtthatók kiszámíthatók illesztőpontok segitségével, vagy felhasználhatók a felvételekhez kiegészítő adatként megadott együtthatók is. Ez utóbbi lehetővé teszi a műholdfelvétel szolgáltatójának, hogy a kameramodell segítségével kiszámítsa az adott felvételhez tartozó polinomegyütthatókat, és nem a kemeramodell paramétereit, hanem csak a polinomhányados függvény együtthatói adja át a felhasználóknak a felvétel utólagos ortorektifikációjának megkönnyítésére (Dial et al., 2001).

A polinomhányados függvények alkalmazását megnehezíti, hogy a nagyobb pontosság eléréséhez magasabb fokszámú polinomokat kell alkalmazni. A magasabb fokszámú polinomokban több együttható szerepel, ezek meghatározásához sok illesztőpont szükséges. A magasabb fokszámú polinomok alkalmazása még a hagyományos polinomiális korrekciós eljárások esetén sem javasolt a polinomfüggvények illesztőpontok közötti bizonytalan viselkedése miatt, és ezt a helyzetet tovább rontja a polinomhányadosok alkalmazása.

Tartalom