- Ferencz Cs. (1978): Electromagnetic wave propagation in inhomogeneous media: Method of inhomogeneous basic modes; Acta Technica Ac. Sci. H., 86(1 2), 79.
- Ferencz Cs., Ferencz O.E., Hamar D. and Lichtenberger J. (2001): Whistler Phenomena, Short Impulse Propagation. Kluwer Academic Publisher, Netherlands, 1-260. ISBN 0-7923-6995-5
- Ferencz O. E. (2005): Full-wave solution of short impulses in inhomogeneous plasma. Pramana Journal of Physics, 64(2), 1-20. ISSN 0304-4289
- Holden D.N., Munson C.P. and Devenport J.C. (1995): Satellite observations of transionospheric pulse pairs; Geophys. Res. Lett., 22, 889.
- O.E. Ferencz et al., Ann.Geophys,25,1103,2007
Villamos jelek terjedése anizotróp plazmában - hullámterjedési modellek
Az űrfizikai alkalmazásokban, hullámkísérletekben rögzített jelformák a mágneses térrel átjárt (anizotróp)
plazmaközegben terjedő elektromágneses hullámok, illetve a közeg saját rezgései (plazmahullámok). A természetes
keltésű emissziók döntő többsége időben korlátos, a jelek belső szerkezetüket tekintve koherensek, vagy ismeretlen
fázisképük miatt struktúrálatlan, zajszerű hullámok. A mágneses és elektromos tér időbeni változását leíró hullámok
általában széles, vagy nagyon széles frekvencia-átfogású (ú.n. ultra wide-band, UWB) hullámcsomagok, impulzusok.
A plazmában terjedő elektromágneses jelek terjedésére általánosan, széles körben használt leírásmód a Fourier-analízis
alapján a jelet független frekvencia összetevők együtteseként kezeli (monokromatikus leírás), e
megközelítésben a jelrészek a közeg helytől és frekvenciától függő törésmutatója által megszabott módon, eltérő
terjedési utakon jutnak a forrástól (gerjesztés) a mérőberendezés szenzoráig. E mellett a monokromatikus modell időben
végtelen harmonikus komponensekkel operál, ami irrelális előfeltétel.
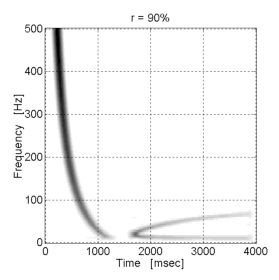
A monokromatikus leírás többrétű elvi és kísérletileg is kimutatható korlátjának feloldására, a mért jelek értelmezésében felhasználható, pontos modell jelalak meghatározására az Űrkutató Csoportban térelméleti, hullámterjedési modellfejlesztés kezdődött a 90-es évek elején. A plazmában terjedő hullámok jelalakjának pontos megadását kitűző új leírásmód a Maxwell-egyenletek megoldásában a jelről, gerjesztésről semmi megkötést nem tartalmaz (teszőleges alakú jelek). E fejlesztés első, Ferencz Csaba által elért eredményei az anizotróp, homogén, illetve gyengén inhomogén [Ferencz Cs, 1978] elektron-plazmában erővonallal párhuzamosan (longitudinálisan) terjedő, tetszőleges (pl. Dirac-delta) gerjesztésű impulzusra adott, zárt alakú megoldások voltak, amik az elektron-whistler időtartományú jelalakját adták koherens impulzus formájában, elsőként a hullámterjedési kutatások történetében. (Megjegyzendő, hogy a tetszőleges alakú (ú.n. full-wave) megoldás gyakran használt megjelölés olyan modellekben is, ahol az impulzust monokromatikus jelcsomagok (wave packet) összegzésével állítják elő, tehát a jel ezekben alapvetően nem impulzus, a modell tisztán monokromatikus annak minden korlátjával.)
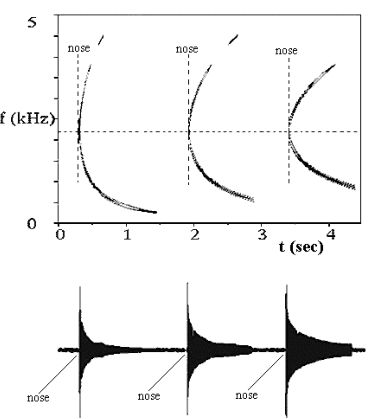
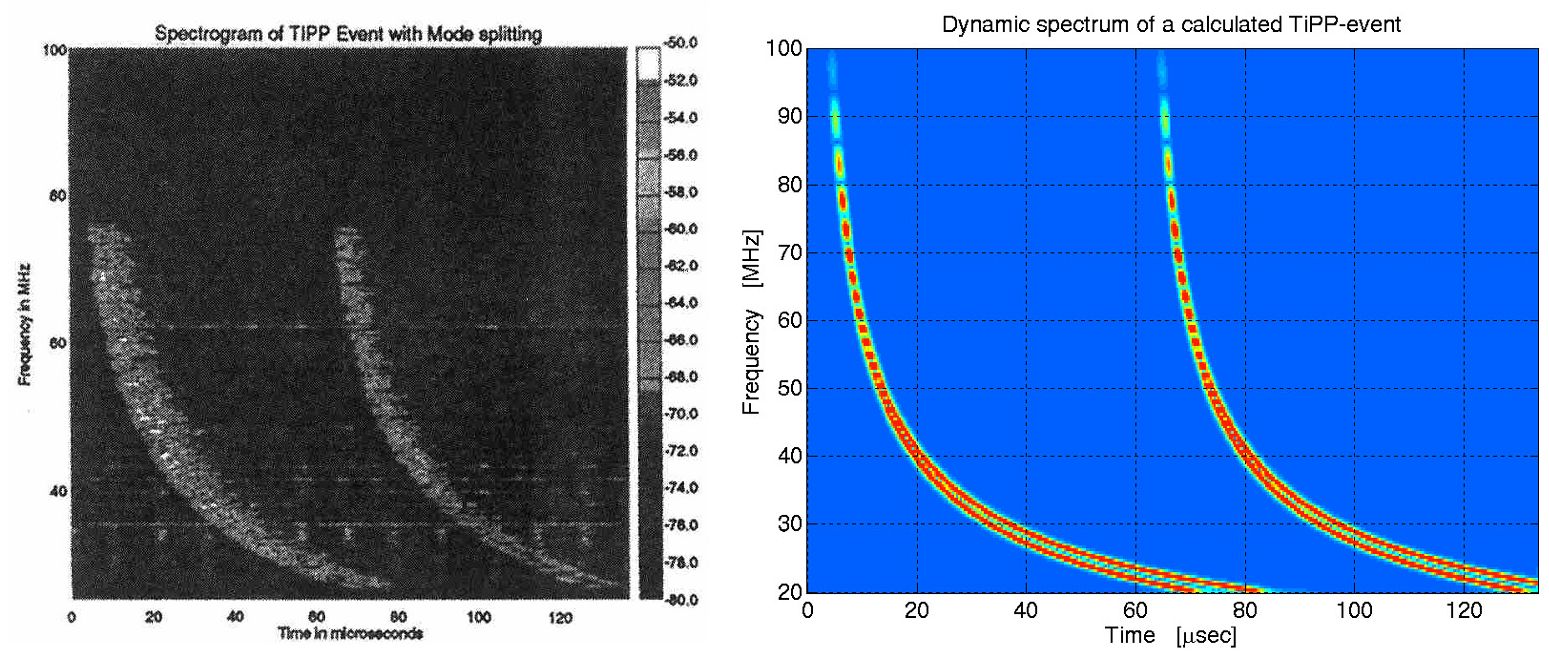
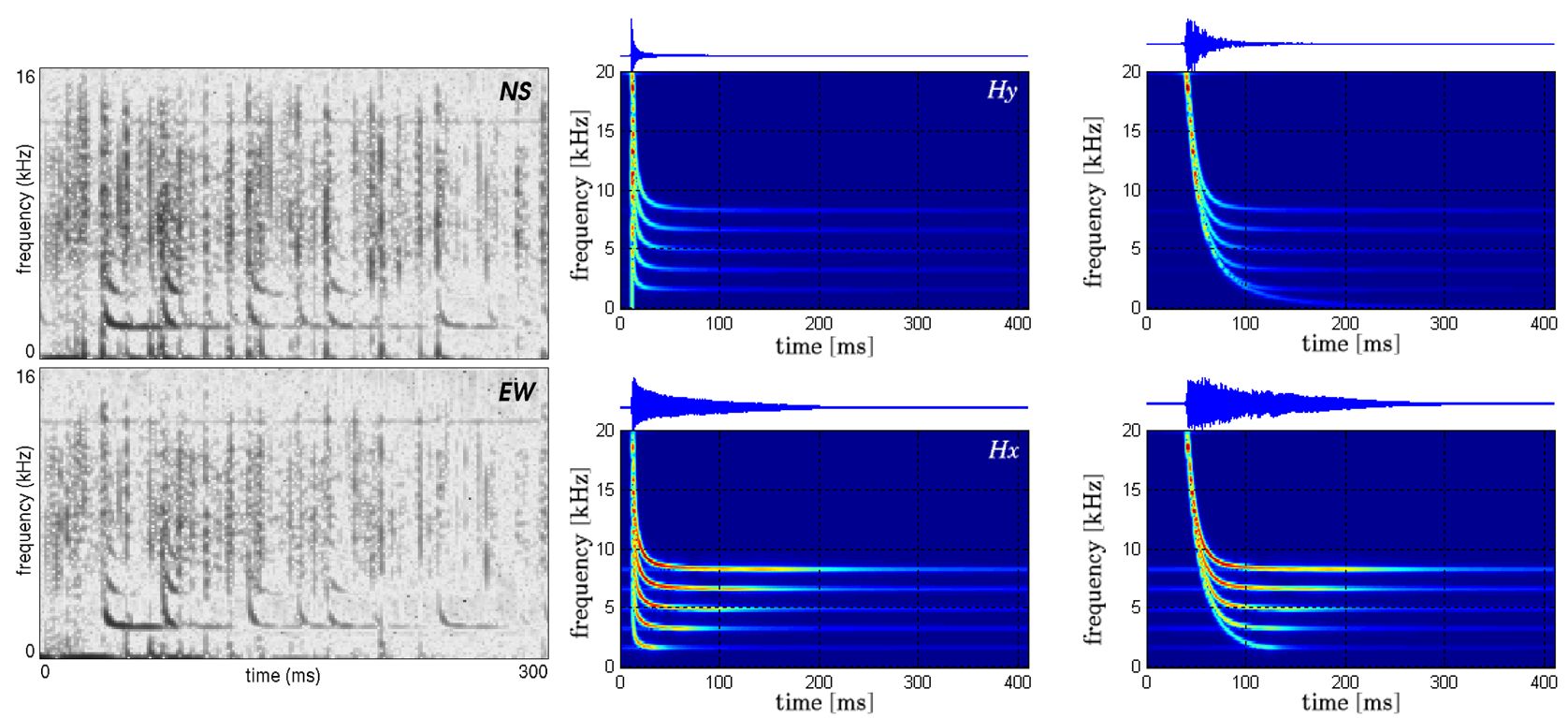
A Maxwell-egyenletek tetszőleges gerjesztésű jelek plazmában terjedésére érvényes modellt továbbfejlesztve Ferencz Orsolya megadta a pontos megoldást a mágneses térrel szöget bezáró (ú.n. ferde terjedés), tetszőleges ionösszetételű plazma (ion-whistler), veszteséges plazmában és egyenes geometriájú vezetőszerkezetben terjedés esetekre [Ferencz et al., 2001.]. Ezt követően - az űrfizikában általánosan előforduló, ezért a tudományos értelmezésben kitüntetett szerepű - inhomogén plazmában terjedés leírása született meg, tetszőleges mértékű inhomogenitások esetére is érvényes alakban. [Ferencz O. 2005]. Ennek a megoldásnak érvényességét nem korlátozza az általánosan használt, de csak gyenge inhomogenitások esetében alkalmazható WKB közelítés.